서론
학습 모델 중에서 가장 심플한 선형 회귀(Linear Regression) 모델에 대해 우선 살펴보자. 해당 모델은 크게 두 분류로 구분할 수 있다. 훈련 세트에 대해 모델을 가장 잘 맞게 하는 모델 파라미터를 직접 계산하는 "closed-form" 방정식을 사용하는 방식과 경사 하강법(Gradient Descent, GD)이라는 반복적인 최적화 접근 방식을 사용하여 점진적으로 모델 파라미터를 조정하여 훈련 세트 상의 비용 함수를 최소화하도록 하는 방식으로 나뉜다. 이외에 선형 회귀를 이용하여 다항 회귀(Polynomial Regression)를 이해하고 마지막으로 분류 작업에 흔히 사용되는 Logistic Regression과 Softmax Regression 두 가지 모델을 살펴볼 것이다.
Linear Regression (선형 회귀)
선형 회귀(Linear Regression)는 데이터에 대한 선형 모델을 사용하여 예측 및 회귀 분석을 수행하는 기초적인 기계 학습 알고리즘이다. 이 알고리즘은 입력 특성들의 가중치 합과 절편(bias term 또는 intercept term)을 간단히 계산하여 예측을 수행한다. 모델을 훈련한다는 것은 모델이 훈련 세트에 가장 잘 맞도록 파라미터를 설정하는 것을 의미한다. 즉, 먼저 모델이 훈련 데이터에 얼마나 잘(또는 나쁘게) 맞는지 측정하는 방법이 필요하다. 이를 위해 평균 제곱근 오차(Root Mean Square Error , RMSE)를 사용한다. 따라서 선형 회귀 모델을 훈련하기 위해서는 RMSE를 최소화하는 θ의 값을 찾아야 한다. 실제로는 RMSE보다 평균 제곱 오차(mean squared error , MSE)를 최소화하는 것이 더 간단하고 동일한 결과를 가져온다.


Normal Equation
노멀 방정식(Normal Equation)은 비용 함수를 최소화하는 θ의 값을 직접적으로 제공하는 수식적인 방법이다. 우선 무작위로 선형 모양의 데이터를 생성하여 노멀 방정식을 테스트한다. 노멀 방정식을 사용하여 𝜃를 계산한다.

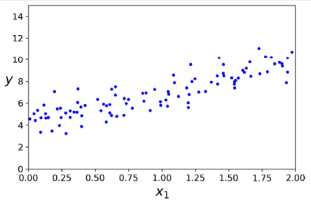
import numpy as np
X = 2 * np.random.rand(100,1)
y = 4 + 3 * X + np.random.rand(100,1)
X_b = np.c_[np.ones((100, 1)), X] # 각 인스턴스에 X0 = 1을 추가
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best # array([[4.21509616],[2.77011339]])위 예시를 보면 노이즈로 인해 원래 함수의 정확한 파라미터를 복구하는 것이 불가능했지만, 𝜃0 = 4, 𝜃1 = 3 대신에 𝜃0 = 4.215, 𝜃1 = 2.770을 얻었다. 이제 𝜃를 사용하여 예측을 할 수 있다.
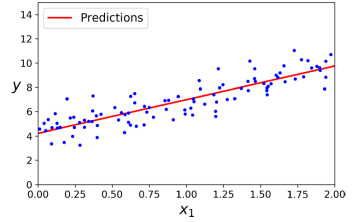
X_new = np.array([[0],[2])
X_new_b = np.c_[np.ones((2,1)), X_new]
y_predict = X_new_b.dot(theta_best)
y_predict # array([[4.21509616],[9.75532293]])
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()Scikit-Learn을 사용하여 선형 회귀를 수행하는 것은 간단하다. LinearRegression 클래스는 scipy.linalg.lstsq() 함수에 기반한다. scipy.linalg.lstsq() 함수는 𝜃 = (X^T * X)^-1 * X^T * y를 계산한다. 여기서 의사 역행렬(pseudoinverse)인 X^T * X^-1은 표준 행렬 분해 기술인 특이값 분해(SVD)를 사용하여 계산된다.
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_ # array([[4.21509616],[2.77011339]])
lin_reg.predict(X_new) # array([[4.21509616],[9.75532293]])
노멀 방정식은 (n + 1) × (n + 1) 행렬(여기서 n은 특성 수)인 X^T * X의 역을 계산한다. 이러한 행렬의 역을 계산하는 계산 복잡도는 일반적으로 약 O(n^2.4)에서 O(n^3)이다. 즉, 특성 수가 두 배가 되면 계산 시간이 약 2^2.4 = 5.3에서 2^3 = 8배가 된다. Scikit-Learn의 LinearRegression 클래스에서 사용하는 SVD(Singular Value Decomposition) 방법은 약 O(n^2)이다. 따라서 특성 수를 두 배로 늘리면 계산 시간이 대략 4배가 된다. 특성 수가 매우 커질 때(예: 100,000) 노멀 방정식과 SVD 접근 방식은 모두 매우 느려진다. 그러나 긍정적인면에서 둘 다 훈련 세트의 인스턴스 수에 대해 선형이므로(즉, O(m)이라고 표현됨) 메모리에 맞는 큰 훈련 세트를 효율적으로 처리할 수 있다.
Gradient Descent (경사 하강법)
Gradient Descent(경사 하강법) 모델의 가중치를 최적화하기 위해 사용되는 최적화 기술로, 다양한 머신러닝 모델의 학습에 쓰인다. 즉, Gradient Descent는 다양한 문제에 최적해를 찾을 수 있는 일반적인 최적화 알고리즘이다. Gradient Descent의 일반적인 아이디어는 비용 함수를 최소화하기 위해 매개변수를 반복적으로 조정하는 것이다. 매개변수 벡터 θ에 대한 오류 함수의 지역 기울기를 측정하고 기울기 하강 방향으로 이동한다. 기울기가 0이 되면 최솟값에 도달한 것이다.
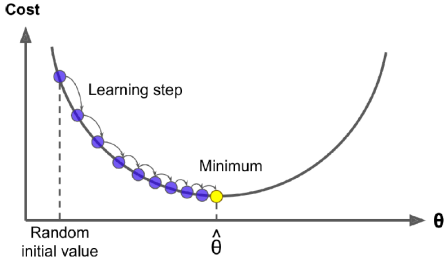
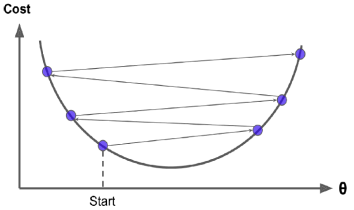
먼저 θ를 무작위 값으로 채운(Random initialization) 다음, 알고리즘이 최소값에 수렴할 때까지 비용 함수(MSE와 같은)를 감소시키기 위해 점진적으로 개선한다. 학습률 하이퍼파라미터는 각 단계의 크기를 나타낸다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 많은 반복을 수행해야 하므로 오랜 시간이 걸릴 수 있다. 반대로 학습률이 너무 높으면 계곡을 건너뛰어 알고리즘이 발산할 수 있다.
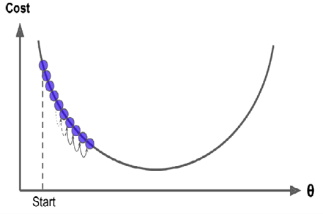
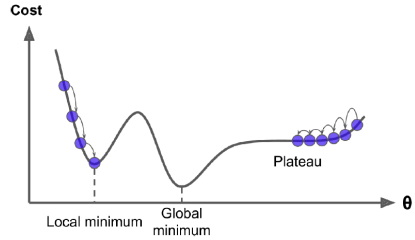
마지막으로 주의해야할 점은 모든 비용 함수가 좋은 정규의 형태가 아닐 수 있다는 것이다. 구멍, 능선, 고원 및 여러 가지 불규칙한 지형이 있어 최솟값으로의 수렴이 어려울 수 있다. 이 때 주의해야할 점은 어느 지점에서 랜덤 초기화를 했는 가이다. 아래 예시 처럼 어느 지점에 시작했느냐에 따라 극값(local minimun)으로 갈 수 있다. 다행히도 MSE의 비용 함수는 볼록 함수이기에 local minimum이 없다.
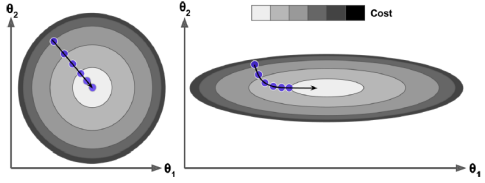
비용 함수가 볼록 함수인 경우 Gradient Descent는 전역 최소값에 임의로 가까이 다가가도록 보장된다(충분히 오랜 시간을 기다리고 학습률이 너무 높지 않은 경우). 사실 비용 함수는 그릇의 모양을 갖지만 특성의 스케일이 매우 다르면 길쭉한 그릇이 될 수 있다. Gradient Descent를 사용할 때 모든 특성이 유사한 스케일을 갖도록(예: Scikit-Learn의 StandardScaler 클래스 사용)해야 수렴하는 데 시간이 덜 걸리도록 해야 한다.
Batch Gradient Descent
배치 경사 하강법을 구현하기 위해서는 각 모델 매개변수 𝜃𝑗에 관한 비용 함수의 그래디언트를 계산해야 한다. 즉, 𝜃𝑗를 조금 변경할 때 비용 함수가 얼마나 변하는지 계산해야 한다. 이를 편도함수(partial derivative)라고 한다.
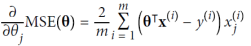

위 식을 보면 비용 함수의 편도함수는 매 경사 하강 단계마다 전체 훈련 세트 X에 대한 계산을 수행한다는 것을 알 수 있다. 매 단계에서 모든 훈련 데이터를 사용하기 때문에 이 알고리즘이 배치 경사 하강법이라고 불린다. 결과적으로 매우 큰 훈련 세트에서는 속도가 굉장히 느리다. 하지만 경사 하강법은 특성의 수에 비례하여 확장되므로 수십만 개의 특성이 있는 경우, 노멀 방정식이나 SVD 분해를 사용하는 것보다 경사 하강법을 사용하여 선형 회귀 모델을 훈련하는 것이 훨씬 빠르다.
eta = 0.1 # 학습률
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # 램던 초기화
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
theta # array([[4.21509616],[2.77011339]]
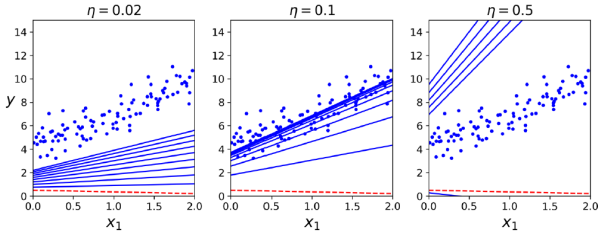
매개변수 업데이트는 𝜂가 학습률을 이용한 공식을 사용한다. 적절한 학습률을 찾기 위해 그리드 서치( grid search)를 사용할 수 있다. 또한 반복 횟수를 어떻게 설정해야 하는지에 알아야 한다. 반복 횟수가 너무 낮으면 알고리즘이 중단될 때 최적 솔루션에서 여전히 멀리 떨어져 있다.(예시 그림에서 n = 0.02) 반대로 너무 높으면 모델 매개변수가 더 이상 변하지 않는 동안 시간을 낭비하게 될 것이다.(예시 그림에서 n = 0.5) 그래서 일반적으로는 충분히 큰 반복 횟수를 설정하지만 그래디언트 벡터의 노름이 아주 작아질 때(즉, 그 노름이 작은 수 𝜖보다 작아질 때) 알고리즘을 중단하는 것으로 간단히 해결한다.
Stochastic Gradient Descent
배치 경사 하강법의 주요 문제점은 모든 단계에서 그레이디언트를 계산하기 위해 전체 훈련 세트를 사용하는 것이다. 따라서 대규모의 훈련 세트인 경우 매우 느리게 작동한다. 이에 비해 확률적 경사 하강법(Stochastic Gradient Descent)은 매 단계에서 훈련 세트에서 무작위로 하나의 인스턴스를 선택하고 해당 단일 인스턴스에 기반하여 그레이디언트를 계산한다. 단일 인스턴스를 처리하는 것은 알고리즘을 매 반복마다 조작해야 할 데이터가 거의 없기 때문에 알고리즘을 훨씬 빠르다. 또한 매 반복마다 메모리에 하나의 인스턴스만 있으면 되기 때문에 대규모 훈련 세트에서도 훈련할 수 있다. 그러나 이 알고리즘의 확률적(즉, 무작위) 성질 때문에 이 알고리즘은 배치 경사 하강법보다 훨씬 덜 규칙적이다. 한편, 학습률을 점진적으로 감소시키는 것은 지역 최솟값에서 벗어나는 데 도움이 되지만 알고리즘이 최솟값에 정착할 수 없다는 문제를 해결하는 한 가지 방법이다. 각 반복에서 학습률을 결정하는 함수를 학습 스케줄이라고 한다.
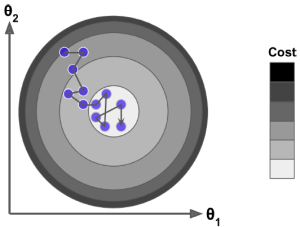
확률적 경사 하강법을 사용할 때는 훈련 인스턴스가 평균적으로 전역 최적값으로 향하도록 독립적이고 동일하게 분포되어 있어야 한다(independent and identically distributed, IID). 인스턴스를 섞지 않으면 예를 들어 인스턴스가 레이블별로 정렬된 경우 SGD는 하나의 레이블에 대해 최적화를 시작한 다음 다음 레이블로 이동하게 되어 전역 최솟값 근처에 안착하지 못할 것이다.
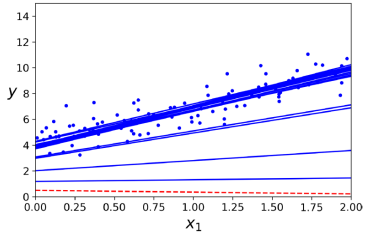
n_epochs = 50
t0, t1 = 5, 50 # 학습 스케줄 하이퍼파라미터
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # 랜덤 초기화
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index + 1]
yi = y[random_index:random_index + 1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedile(epoch * m + i)
theta = theta - eta * gradients
theta # array([[4.21076011],[2.74856079]])
Scikit-Learn 을 사용하여 확률적 경사 하강법을 사용하여 선형 회귀를 수행하려면 SGDRegressor 클래스를 사용할 수 있다.
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter = 1000, tol = 1e-3, penalty = None, eta0 = 0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_ # array([4.24365286]), array([2.8250878])Mini-batch Gradient Descent
미니 배치 경사 하강법(Mini-batch Gradient Descent)은 미니 배치라고 하는 작은 무작위 인스턴스 집합에서 그레이디언트를 계산한다. 미니 배치 GD의 주요 장점은 특히 GPU를 사용할 때 행렬 연산의 하드웨어 최적화로부터 성능 향상을 얻을 수 있다.

Mini-batch Gradient Descent은 매우 큰 미니 배치를 사용할 때 Stochastic GD보다 매개변수 공간에서의 진행이 덜 불규칙적이다. 배치 GD의 경로는 실제로 최솟값에서 멈춘다. 반면 확률적 GD와 미니 배치 GD는 여전히 최솟값 주변을 계속 돌아다닌다. 그러나 각 단계를 수행하는 데 Batch GD에는 많은 시간이 걸리며, 만약 좋은 학습 스케줄을 사용한다면 확률적 GD와 미니 배치 GD도 최솟값에 도달할 수 있다.
Linear Regression 알고리즘 비교
| Algorithm | Large m | Out-of-core support(메모리가 부족해도) | Large n | Hyperparams | (input feature) scaling required | Scikit-Learn |
| Normal Equation | 빠름 | No | 느림 | 0 | No | N/A |
| SVD | 빠름 | No | 느림 | 0 | No | Linear Regression |
| Batch GD | 느림 | No | 빠름 | 2 | Yes | SGDRegressor |
| Stochastic GD | 빠름 | Yes | 빠름 | >= 2 | Yes | SGDRegressor |
| Mini-batch GD | 빠름 | Yes | 빠름 | >= 2 | Yes | SGDRegressor |
n: features(특성)의 갯수, m: 데이터 인스턴스의 개수
Polynomial Regression (다항 회귀)
데이터가 직선보다 더 복잡하고 비선형 데이터에서도 선형 모델을 사용할 수 있다. 이를 위한 간단한 방법은 각 특성의 제곱을 새로운 특성으로 추가한 다음 이 확장된 특성 집합에 선형 모델을 훈련하는 것이다. 이 기술을 다항 회귀(Polynomial Regression)라고 한다. 다항 회귀는 선형 회귀(Linear Regression) 모델을 확장하여 다항식 함수로 데이터를 모델링하는 회귀 기술이다.
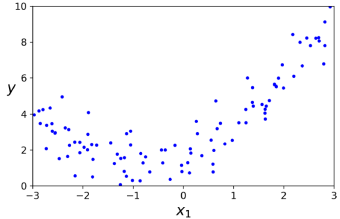
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.rand(m, 1)간단한 이차 방정식에 노이즈를 더한 비선형 데이터를 생성해 보자. 이 경우에는 특성이 하나뿐이므로 훈련 세트에 각 특성의 제곱(이차 다항식)을 새로운 특성으로 추가하기 위해 Scikit-Learn의 PolynomialFeatures 클래스를 사용해 보자.
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree = 2, include_bias = False)
X_poly = poly_features.fit_transform(X)
X[0] # array([-0.75275929])
X_poly[0] # array([-0.75275929, 0.56456263])이 확장된 훈련 데이터에 LinearRegression 모델을 적합시켜 보자.
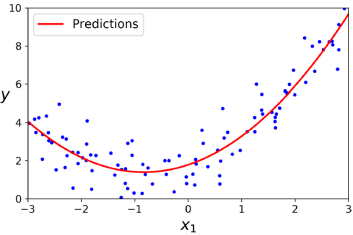
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_ # array([1.78134581]), array([[0.93366893, 0.56456263]])여러 특성(features)이 있는 경우 Polynomial Regression은 특성 간의 관계를 찾을 수 있다. 이는 PolynomialFeatures가 주어진 차수까지의 모든 특성 조합을 추가하기 때문에 가능하다. 예를 들어, 특성 두 개 𝑎와 𝑏가 있는 경우, 차수가 3인 PolynomialFeatures는 𝑎^2, 𝑎^3, 𝑏^2 , 𝑏^3과 함께 𝑎𝑏, 𝑎^2𝑏, 𝑎𝑏^2와 같은 조합을 추가한다. 단, 특성 수가 급격하게 증가하는 조합 폭발에 주의해야 한다. PolynomialFeatures(degree = d)는 𝑛 개의 특성을 포함하는 배열인 경우 (𝑛 + 𝑑!) / (𝑑!𝑛!) 특성을 포함하는 배열로 변환하기 때문이다.
Learning Curves (학습 곡선)
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size = 0.2)
train_erros, val_erros = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_erros), "r-+", linewidth = 2, label = "train")
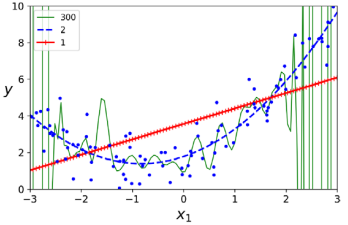
plt.plot(np.sqrt(val_erros), "b-", linewidth = 3, label = "val")모델이 얼마나 복잡해야 하는지 결정하는 방법은 무엇일까? 높은 차수의 다항 회귀는 일반적으로 일반 선형 회귀보다 훈련 데이터에 훨씬 잘 맞을 것이다. 그러나 훈련 데이터를 심하게 과적합하고, 선형 모델은 과소적합된다. 이를 결정하는 데 도움을 주는 것이 학습 곡선(Learning Curves)이다. 학습 곡선은 모델의 성능을 평가하기 위해 데이터 크기(훈련 세트 크기 또는 훈련 반복)에 따른 학습 및 검증 세트의 성능을 시각화하는 방법이다. 학습 곡선을 생성하려면 여러 번의 훈련 세트 하위 집합에서 모델을 여러 번 훈련해야 한다.
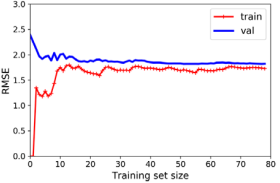
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)일반 선형 회귀 모델의 학습 곡선을 살펴보자. 이 곡선은 과소적합(underfitting)되었다. 훈련 세트에 하나 또는 두 개의 인스턴스만 있는 경우 모델은 이를 완벽하게 맞출 수 있기 때문에 곡선이 0에서 시작한다. 그러나 새로운 인스턴스가 훈련 세트에 추가되면 데이터가 매우 노이즈가 많고 전혀 선형적이지 않기 때문에 모델이 훈련 데이터를 완벽하게 맞추는 것은 불가능하다. 따라서 훈련 데이터의 오류는 플래토에 도달할 때까지 증가한다. 이때, 새로운 인스턴스를 훈련 세트에 추가해도 평균 오류가 크게 나빠지거나 좋아지지 않는다. 즉, 과속적합의 특징으로 두 곡선의 거리가 가깝다는 것이다.
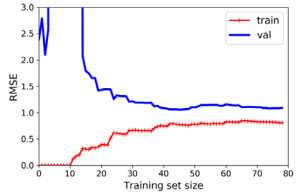
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree = 10, include_bias = False)),
("lin_reg", LinearRegression())
])
plot_learning_curves(polynomial_regression, X, y)
동일한 데이터에 대한 10차 다항 모델의 학습 곡선을 살펴보자. 이 곡선은 과적합(overfitting)되었다. 이전 그래프와 매우 중요한 두 가지 차이점이 있다. 첫째, 훈련 데이터의 오류는 일반 선형 회귀 모델보다 훨씬 낮다. 둘째, 두 곡선 사이에 격차가 있다. 이는 모델이 훈련 데이터에서 검증 데이터보다 훨씬 더 잘 수행된다는 것을 의미한다. 그러나 훨씬 더 큰 규모의 훈련 세트를 사용하면 두 곡선이 점점 가까워질 것이다.
Regularized Linear Models (정규화된 선형 모델)
정규화(Regularization)는 과적합을 줄이는 좋은 방법이다. 이는 모델의 자유도를 줄이는 것을 의미한다. 다항식 모델을 정규화하는 간단한 방법은 다항식 차수를 줄이는 것이며 선형 모델의 경우, 정규화는 일반적으로 모델의 가중치를 제한함으로써 달성된다.
Ridge Regression
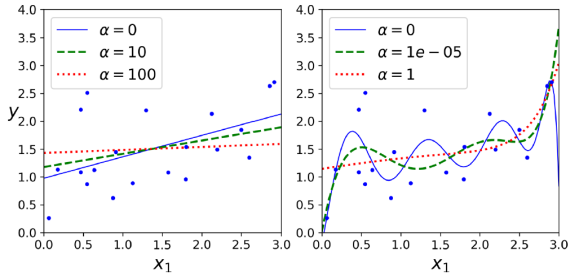

Ridge Regression은 L2 규제를 사용하여 모델의 가중치를 조정한다. 이는 비용 함수에 페널티 항(1/2𝛼∑ 𝜃^2𝑖 )을 추가함으로써 모델의 가중치가 큰 값을 취하지 않도록 제한한다. 이러한 규제는 가중치를 0에 가깝게 유지하게 만들지만 정확히 0으로 만들지는 않는다. 따라서 Ridge Regression은 변수들을 모델에 유지하면서 그들의 영향력을 줄이는 방법이다. 이는 다중공선성 문제를 완화하는 데 도움이 된다.
하이퍼파라미터 𝛼는 모델을 정규화하는 정도를 제어한다. 만약 𝛼 = 0이라면, Ridge 회귀는 단순히 선형 회귀와 같다. 만약 𝛼가 매우 크다면, 모든 가중치가 0에 아주 가까워지고 결과적으로 데이터의 평균을 통과하는 평평한 선이 된다.(참고로 편향 항 𝜃0은 정규화되지 않는다.) Ridge 회귀를 수행하기 전에 데이터를 척도화하는 것(예: StandardScaler 사용)이 중요하며, 이는 대부분의 정규화된 모델에 해당된다.
Lasso Regression
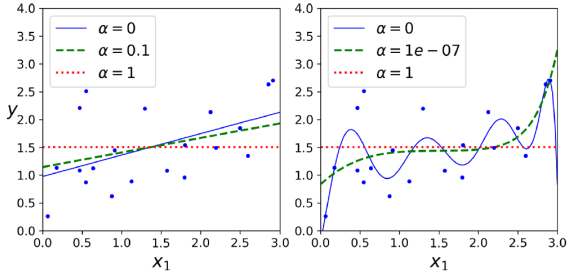

Lasso Regression는 비용 함수에 정규화 항을 추가하지만, 이때 ℓ2 노름의 절반 대신에 가중치 벡터의 ℓ1 노름을 사용하여 모델의 가중치를 조절한다. Lasso 회귀의 중요한 특징은 가장 중요하지 않은 특성들의 가중치를 제거하려는 경향(가중치를 0으로 설정한다) 이 있다는 것이다. 즉, , 라쏘 회귀는 자동으로 특성 선택을 수행하고 희소한 모델 (거의 없는 특성 가중치를 갖는 모델)을 출력한다. 이를 통해 중요하지 않은 변수를 모델에서 제외시킬 수 있다. 이러한 특징은 변수 선택이 필요한 상황에서 유용하다.
Ridge vs. Lasso Regression
Ridge Regression과 Lasso Regression은 각각의 특징에 따라 다양한 상황에서 유용하게 사용된다. 선택하기 전에 데이터와 문제의 특성을 고려하여 적합한 규제 방법을 선택하는 것이 중요하다.
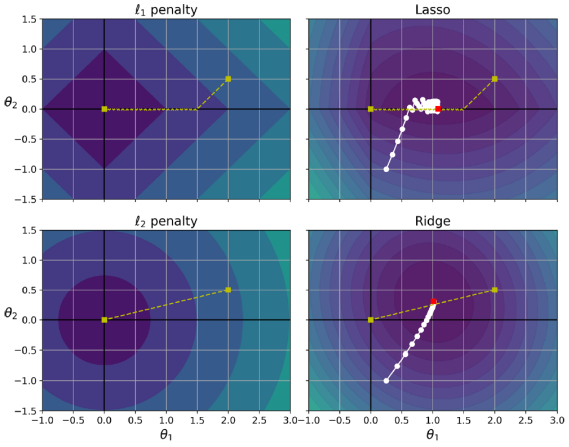
Elastic Net
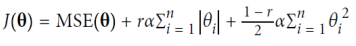
신축망(Elastic Net)은 릿지 회귀와 라쏘 회귀 사이의 절충안이다. 정규화 항은 릿지와 라쏘의 정규화 항을 간단히 혼합한 것이며, 혼합 비율 𝑟을 조절할 수 있다. 𝑟 = 0일 때, 탄력적 넷은 릿지 회귀와 동일하며, 𝑟 = 1일 때, 라쏘 회귀와 동일하다.
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha = 0.1, l1_ratio = 0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]]) # array([1.5433232])Early Stopping
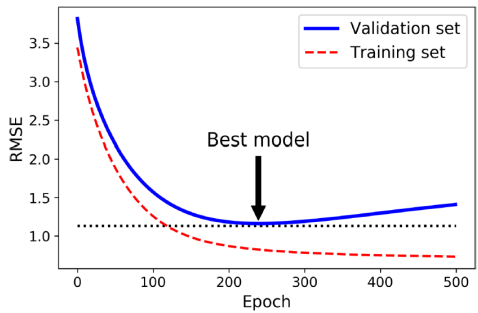
조기 종료(Early Stopping)는 그라디언트 디센트와 같은 반복 학습 알고리즘을 규제하는 매우 다른 방법이다. 이는 검증 오차가 최솟값에 도달하면 훈련을 중지하는 것이다.
from sklearn.base import clone
# 데이터 준비
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree = 90, include_bias = False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter = 1, tol = -np.infty, warm_start = True,
penalty = None, learniong_rate = "constant", eta0 = 0.0005)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # continues where it left off
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)Logistic Regression (로지스틱 회귀)
분류 문제에 사용되는 회귀 기술로, 데이터를 클래스에 할당하는 데 사용된다.
확률 추정(Estimating Probabilities)

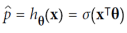
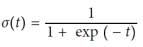
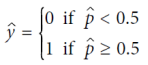
확률을 추정하는 몇 가지 회귀 알고리즘은 분류에 사용될 수 있다. 그중 하나가 로지스틱 회귀(Logistic regression)이다. 이는 특정 클래스에 속할 확률을 추정하는 데 자주 사용된다. 선형 회귀 모델과 유사하게 로지스틱 회귀 모델은 입력 특성의 가중 합(바이어스 항을 포함)을 계산하지만, 선형 회귀 모델이 결과를 직접 출력하는 대신 로지스틱 함수의 결과를 출력한다. 로지스틱 함수는 시그모이드 함수로 표현되며, 로지스틱 회귀 모델이 인스턴스 x가 양성 클래스에 속할 확률 p^=h_θ(x)를 추정한 후, 예측 y^을 쉽게 할 수 있다.
교육 및 비용 함수(Training and Cost Function)
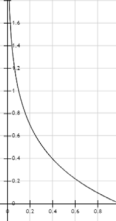
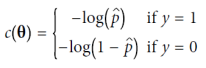


로지스틱 회귀 모델의 학습 목표는 매개 변수 벡터 θ를 설정하여 양성 인스턴스(클래스가 1인 경우)에 대해 높은 확률을 추정하고 음성 인스턴스(클래스가 0인 경우)에 대해 낮은 확률을 추정하는 것이다. 이때 -log(t)는 t가 0에 가까워질수록 매우 큰 값을 가지므로, 모델이 양성 인스턴스에 대해 0에 가까운 확률을 추정하면 비용이 크게 증가하며, 음성 인스턴스에 대해 1에 가까운 확률을 추정하면 비용이 커진다. 반대로, -log(t)는 t가 1에 가까워질수록 0에 가까워지므로, 추정된 확률이 음성 인스턴스에 대해 0에 가깝거나 양성 인스턴스에 대해 1에 가까우면 비용이 0에 가까워진다. 전체 학습 세트에 대한 비용 함수는 모든 학습 인스턴스에 대한 평균 비용이며, 이 비용 함수를 최소화하는 θ의 값을 계산하기 위한 닫힌 형식(closs form)의 방정식은 알려져 있지 않다. 그러나 이 비용 함수는 볼록 함수이므로 Gradient Descent(또는 다른 최적화 알고리즘)을 사용하면 학습률이 너무 크지 않고 충분한 시간을 기다린다면 전역 최솟값을 찾을 수 있다.
결정 경계(Decision Boundaries)


# 데이터 불러오기
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys()) # ['data', 'target', 'targer_names', 'DESCR', 'feature_names', 'filename']
X = iris["data"][:, 3:] # 꽃잎 너비
y = (iris["target"] == 2).astype(np.int) # Iris virginica종 이면 1, 아니면 0
# Logistic Regression model 학습
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label = "Iris virginica")
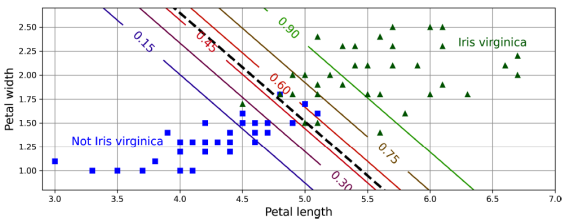
plt.plot(X_new, y_proba[:, 0], "b-", label = "Not Iris virginica")아이리스 데이터셋은 꽃받침과 꽃잎의 길이 및 너비를 포함하며, Iris setosa, Iris versicolor, Iris virginica라는 세 가지 다른 종류의 아이리스 꽃에 대한 150개의 데이터를 담고 있다. 이 데이터를 활용하여 꽃잎의 너비만을 기반으로 Iris virginica 유형을 감지하는 분류기를 구축했다. Iris virginica의 꽃잎 너비는 1.4cm에서 2.5cm까지 범위 하며, 다른 아이리스 꽃은 0.1cm에서 1.8cm까지의 작은 꽃잎 너비를 가지고 있다(일부 겹침이 있음). 분류기는 2cm 이상에서 확신을 갖고 Iris virginica로 판단하며, 1cm 미만에서는 확신을 갖고 Iris virginica가 아님으로 판단한다. 두 극단 사이에서는 확신이 없지만, 예측을 요청하면 가장 가능성이 높은 클래스를 반환한다. 아래 그림은 같은 데이터셋을 이용하되 꽃잎의 너비와 길이 두 가지 특성을 표시하며, 점선은 모델이 50% 확률을 추정하는 지점으로, 이는 모델의 결정 경계를 나타낸다.
소프트맥스 회귀(Softmax Regression)

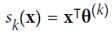
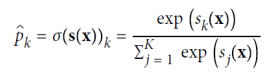

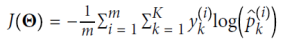
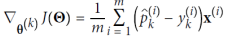
X = iris["data"][:, (2, 3)] # 꽃잎 길이와 너비
y = iris["target"]
softmax_reg = LogisticRegression(multi_class = "multinomial", solver = "lbfgs", C = 10)
softmax_reg.fit(X, y)
softmax_reg.predict([[5,2]]) # array([2])
softmax_reg.predict_proba([[5,2]]) # array([[6.38014896e-07, 5.7492995e-02, 9.42506362e-01]])소프트맥스 회귀는 여러 클래스를 직접 지원하며, 이진 분류기를 여러 개 훈련하고 결합할 필요가 없다. 모델은 각 클래스에 대한 점수를 계산한 뒤, 소프트맥스 함수를 적용하여 각 클래스의 확률을 추정한다. 이때 각 클래스는 고유한 매개 변수 벡터를 가지며, 이들은 보통 매개 변수 행렬에 저장된다. 이 확률 추정을 통해 모델은 각 인스턴스가 어떤 클래스에 속할지 예측한다. 목표는 모델이 특정 클래스에 대해 높은 확률을, 다른 클래스에 대해 낮은 확률을 추정하도록 하는 것이다. 이를 위해 교차 엔트로피라는 비용 함수를 최소화해야 하는데, 이는 모델이 대상 클래스에 대해 낮은 확률을 추정할 때 페널티를 주도록 한다. 이 비용 함수의 그래디언트 벡터를 계산한 뒤, 경사 하강법을 사용하여 비용 함수를 최소화하는 매개 변수 행렬을 찾을 수 있다. 이를 통해 소프트맥스 회귀를 사용하여 아이리스 꽃을 세 가지 클래스로 분류할 수 있다. 예를 들어, 꽃잎이 5cm이고 너비가 2cm인 아이리스는 아이리스 버지니카로 94.2%의 확률로 분류될 수 있다.
주섬주섬
해당 블로그는 수학적인 이해 보다 기계학습에 대한 이해를 초점에 두고 있어. 수학적인 설명을 줄였다. 만약 수학적인 이해가 필요하다면 고등수학, 선형대수, 알고림즘을 공부하고 오는 것을 추천한다.
참고
iris data는 기계학습의 대표적인 예시 데이터 샘플이다.
Iris flower data set - Wikipedia
From Wikipedia, the free encyclopedia Statistics dataset Scatterplot of the data set The Iris flower data set or Fisher's Iris data set is a multivariate data set used and made famous by the British statistician and biologist Ronald Fisher in his 1936 pape
en.wikipedia.org
Iris Species
Classify iris plants into three species in this classic dataset
www.kaggle.com
'컴퓨터공학 > AI' 카테고리의 다른 글
| 기계 학습 6. 의사 결정 트리(Decision Trees) (1) | 2023.10.19 |
|---|---|
| 기계 학습 5. Support Vector Machine(SVM) (1) | 2023.10.19 |
| 기계 학습 3. 분류(Classification) (0) | 2023.09.20 |
| 기계 학습 2.프로젝트 진행 과정 (0) | 2023.09.18 |
| 기계 학습 1.기본 개념 (0) | 2023.09.13 |




댓글