서론
SVM(Support Vector Machine)은 지도 학습 알고리즘 중 하나로, 주어진 데이터를 기반으로 분류 또는 회귀 분석을 할 수 있는 알고리즘이다. 주로 분류 작업에 사용되며, 결정 경계를 찾고 데이터를 클래스로 분류하는 데 중점을 둔다. SVM은 주어진 데이터를 가장 잘 분류하는 경계를 찾는 것이 목표이며, 이를 위해 데이터 포인트 사이의 간격(마진)을 최대화하려고 노력한다. 이러한 알고리즘은 선형 및 비선형 문제에 모두 적용할 수 있으며, 커널 트릭을 사용하여 고차원 공간으로 데이터를 변환하여 분류 작업을 수행할 수 있다. SVM은 이상치에 강한 경향이 있고, 비교적 적은 데이터로도 잘 일반화될 수 있는 강력한 모델이다.
Linear SVM Classification

선형 SVM 분류(Linear SVM Classification)는 SVM(Support Vector Machine)의 기본적인 아이디어에 근거한다. 두 클래스가 명확하게 분리되는 경우, 직선으로 쉽게 구분할 수 있다.(여러 개의 결정 경계가 존재할 수 있다.) 위 그림 중 왼쪽 그림에서 두 모델(실선 결정 경계)은 훈련 세트에서 완벽하게 작동하지만, 결정 경계(decision boundary)가 인스턴스에 너무 가까워서 새로운 인스턴스에 대해 성능이 그리 좋지 않을 가능성이 있다. 오른쪽 그림에서는 실선이 SVM 분류기의 결정 경계를 나타내며, 이 직선은 두 클래스를 분리하는 것뿐만 아니라 가능한 한 가장 멀리 떨어져 있다. 이를 큰 마진 분류(large margin classification)라고 할 수 있다. 새로운 훈련 인스턴스를 "거리 밖"(off the street)에 추가해도 결정 경계에는 영향을 미치지 않는다.(마진 밖) 이는 완전히 해당 범위에 존재하는 인스턴스에 의해 결정된다. 이러한 인스턴스(마진 안)를 서포트 벡터(support vectors)라고 한다. 이들은 오른쪽 그림에서 원으로 표시되어 있다.

SVM은 특성(feature) 스케일에 민감하다. 왼쪽 그림에서 수직 스케일이 수평 스케일보다 훨씬 크기 때문에 가장 넓은 거리는 수평에 가깝다. 오른쪽 그림에서는 특성 스케일링 후 결정 경계가 훨씬 좋아 보인다.
Soft Margin Classification

소프트 마진 분류는 하드 마진 분류의 두 가지 주요 문제를 피하기 위해 더 유연한 모델을 사용한다. 첫째, 데이터가 선형적으로 구분 가능한 경우에만 작동한다. 둘째, 아웃라이어(outliers)에 민감하다. 목표는 거리를 최대한 넓게 유지하면서 마진 위반(margin violations , 거리 중간이나 잘못된 쪽에 있는 인스턴스)을 제한하는 것이다.

import numpy as np
from sklearn implort datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # 꽃잎 길이와 너비
y = (iris["target"] == 2).astype(np.float64) # 꽃받침
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C = 1, loss = "hinge"))
])
svm_clf.fit(X, y)
svm_clf.predict([[5.5, 1.7]]) # array([1.])Scikit-Learn의 SVM 모델의 하이퍼파라미터 C를 사용하여 조정한다. 낮은 값으로 설정하면 왼쪽 모델처럼 되고, 높은 값으로 설정하면 오른쪽 모델처럼 된다. 마진 위반은 좋지 않으며 가능한 적게 발생하는 것이 일반적으로 좋다. 그러나 이 경우 왼쪽 모델은 많은 마진 위반을 가지고 있지만 일반화가 더 잘될 것이다. SVM 모델이 과적합된 경우에는 C 값을 줄여 정규화를 시도할 수 있다. Scikit-Learn 코드를 사용하여 iris 데이터셋을 로드하고 특성을 스케일링한 다음, C=1 및 hinge loss function를 사용하여 선형 SVM 모델을 훈련하여 Iris virginica 품종을 감지한다. LinearSVC 클래스는 바이어스 항을 정규화하므로 훈련 세트를 먼저 평균을 빼서 중심을 맞추어야 한다. 이는 StandardScaler를 사용하여 데이터를 스케일링하면 자동으로 수행된다. 또한 기본값이 아닌 "hinge"로 손실 하이퍼파라미터를 설정해야 한다. 마지막으로, 더 많은 특성이 훈련 인스턴스보다 많은 경우가 아니라면, 듀얼 하이퍼파라미터를 False로 설정하는 것이 성능을 높이는 데 도움이 된다.
Nonlinear SVM Classification

비선형 데이터셋을 처리하는 한 가지 방법은 다항 특성과 같은 더 많은 특성을 추가하는 것이다. 이를 통해 선형적으로 구분 가능한 데이터셋으로 변환될 수 있다. 왼쪽 그림은 선형으로 분리할 수 없는 데이터셋을 보여주고, 오른쪽 그림은 𝑥1^2 = 𝑥1을 추가하여 결과적으로 완벽하게 선형으로 분리할 수 있는 데이터셋을 보여준다. 이 아이디어를 Scikit-Learn을 사용하여 구현하려면 PolynomialFeatures 변환기를 포함하는 Pipeline을 만들면 된다. 이를 moons 데이터셋에 적용해보자.

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
X, y = make_moons(n_samples = 100, noise = 0.15)
polynomial_svm_clf = Pipeline([
("poly_features", Polynomialfeatures(degree = 3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C = 10, loss = "hinge"))
])
polynomial_svm_clf.fit(X,y )Polynomial Kernel

from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel = "poly", degree = 3, coef0 = 1, C = 5))
])
poly_kernel_svm_clf.fit(X, y)다항식 특성을 추가하는 데 두 가지 문제가 있다. 첫째로, 낮은 다항식 차수에서는 매우 복잡한 데이터셋을 처리할 수 없다. 둘째로, 높은 다항식 차수에서는 모델이 너무 느려질 정도로 방대한 수의 특성이 생성된다. 다행히 SVM을 사용할 때 커널 트릭(kernel trick)이라는 거의 기적적인 수학적 기법을 적용할 수 있다. 커널 트릭을 사용하면 실제로 특성을 추가하지 않고도 많은 다항식 특성을 추가한 것과 동일한 결과를 얻을 수 있다. 따라서 실제로 특성을 추가하지 않기 때문에 특성 수의 조합 폭발이 발생하지 않는다. moons 데이터셋에서 이를 테스트해보자.
위 코드는 3차 다항식 커널을 사용하여 SVM 분류기를 훈련시킨다. 모델이 과적합하는 경우 다항식 차수를 줄이고, 모델이 과소적합하는 경우 다항식 차수를 늘렸다. coef0 하이퍼파라미터는 고차 다항식 대비 저차 다항식이 모델에 얼마나 영향을 미치는지를 제어한다.
Similarity Features


비선형 문제를 해결하는 또 다른 기술은 특정 landmark와 각 인스턴스가 얼마나 닮았는지를 측정하는 유사도 함수(similarity function)를 사용하여 생성된 특성을 추가하는 것이다. 예를 들어, 이전에 논의한 1차원 데이터셋에 x1 = -2 및 x1 = 1에 landmark를 추가하자. 그런 다음 γ = 0.3인 가우시안 방사 기저 함수(Radial Basis Function, RBF)를 유사도 함수로 정의할 수 있다. 이 유사도 함수는 0(landmark에서 아주 멀리 떨어진 지점)에서 1(landmark에서의 지점)까지 변화하는 종 모양 함수이다. 이제 새로운 특성을 계산해보자. 우선 x1 = -1인 인스턴스를 살펴보자. 이 인스턴스는 첫 번째 landmark로부터 거리가 1이고 두 번째 landmark로부터 거리가 2에 위치한다. 따라서 x1의 새로운 특성은 𝑥2 = exp(-0.3 × 1^2) ≈ 0.74와 𝑥3 = exp(-0.3 × 2^2) ≈ 0.30이다. 오른쪽 그림은 변환된 데이터셋(원래의 특성을 제거함)을 보여준다. 보시다시피, 이제 선형으로 분리할 수 있다.
landmark를 어떻게 선택해야 할까? 가장 간단한 방법은 데이터셋의 각 인스턴스 위치에 landmark를 만드는 것이다. 이렇게 하면 많은 차원이 생성되어 변환된 훈련 세트가 선형으로 분리될 가능성이 높아진다. 단점으로는 m 개의 인스턴스와 n 개의 특성이 있는 교육 세트가 (원래의 특성을 삭제한다고 가정할 때) m 개의 인스턴스와 m 개의 특성으로 변환된다는 것이다. 즉, 교육 세트가 매우 큰 경우 동일한 수의 특성을 생성된다.
Gaussian RBF Kernel
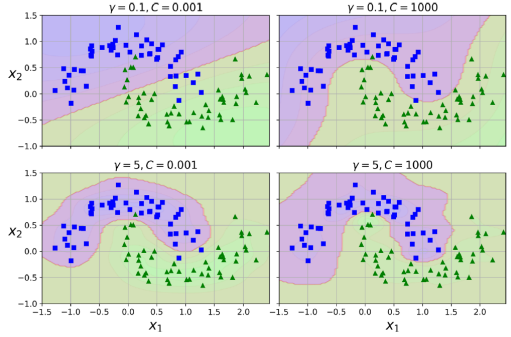
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel = "rbf", gamma = 5, C = 0.001))
])
rbf_kernel_svm_clf.fit(X, y)가우시안 RBF 커널(Gaussian RBF Kernel)에 대해 알아보자. 다항 특성 방법과 마찬가지로 유사도 기능 방법은 모든 기계 학습 알고리즘에 유용할 수 있지만 특히 대규모 교육 세트에서 모든 추가 기능을 계산하는 데는 계산 비용이 많이 들 수 있다. 다시 한번 커널 트릭(kernel trick)이 SVM의 마법을 펼쳐서 추가된 많은 유사도 기능을 추가한 것처럼 유사한 결과를 얻을 수 있게 해준다. 위 코드는 SVC 클래스를 가우시안 RBF 커널로 시도한 코드이다.
하이퍼파라미터 𝛾를 살펴보자. 𝛾를 증가시키면 종 모양 곡선이 좁아져서 각 인스턴스의 영향 범위가 작아지므로 결정 경계(decision boundary)가 각 인스턴스를 중심으로 뒤틀리면서 더 불규칙해진다. 그렇기에 과적합의 가능성이 있다. 반대로 𝛾를 감소시키면 종 모양 곡선이 넓어져서 각 인스턴스의 영향 범위가 커지므로 결정 경계가 더 부드러워진다. 그러나 과소적합의 가능성이 있다.
Other Kernels
다른 커널에 대해 알아보자. 다른 커널은 더 드물게 사용된다. 일부 커널은 특정 데이터 구조에 특화되어 있다. 문자열 커널(String kernels)은 텍스트 문서나 DNA 서열을 분류할 때 사용되기도 한다(예: 문자열 부분 서열 커널이나 Levenshtein 거리를 기반으로 하는 커널 등).
이 많은 커널 중 어떻게 알맞은 커널을 선택해야 할까? 경험적 규칙으로, 특히 교육 세트가 매우 크거나 많은 기능을 가지고 있을 때는 항상 먼저 선형 커널을 시도해 보자. 교육 세트가 그리 크지 않다면 가우시안 RBF 커널도 시도해 보자. 대부분의 경우 잘 작동한다. 그런 다음 여유 시간과 컴퓨팅 파워가 있다면 교차 검증과 그리드 서치를 사용하여 몇 가지 다른 커널을 실험해 볼 수 있다.
Computational Complexity
LinearSVC 클래스는 liblinear 라이브러리를 기반으로 한다. 이 라이브러리는 커널 트릭을 지원하지 않지만 교육 인스턴스 수와 기능 수에 거의 선형적으로 확장된다.SVC 클래스는 커널 트릭을 지원하는 libsvm 라이브러리를 기반으로 한다. 교육 시간 복잡도는 𝑂(𝑚^2 × 𝑛)과 𝑂(𝑚^3 × 𝑛) 사이에 있다. 이는 교육 인스턴스 수가 많아지면 굉장히 느려진다. 이 알고리즘은 복잡한 소규모 또는 중규모의 교육 세트에 적합하다.
| Class | 시간 복잡도 | Out of core support | Scaling required | Kernel trick |
| LinearSVC | O(m × n) | No | Yes | No |
| SGDClassifier | O(m × n) | Yes | Yes | No |
| SVC | 𝑂(𝑚^2 × 𝑛) ~ 𝑂(𝑚^3 × 𝑛) | No | Yes | Yes |
SVM Regression
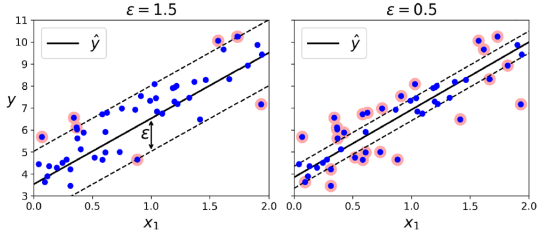
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon = 1.5)
svm_reg.fit(X, y)SVM은 선형 및 비선형 회귀를 지원한다. SVM 회귀를 사용하려면 목적을 반대로 설정해야 한다. 즉, 마진 위반을 제한하면서 가능한 한 많은 인스턴스를 거리 위에 맞추려고 한다.(마진 안이여야 한다.) 거리의 폭은 하이퍼파라미터 ϵ에 의해 제어된다. 마진 내의 더 많은 교육 인스턴스를 추가해도 모델의 예측에 영향을 미치지 않으므로 모델은 ϵ-insensitive이라고 한다. 선형 SVM 회귀를 수행하려면 Scikit-Learn의 LinearSVR 클래스를 사용할 수 있다. 비선형 회귀 작업을 처리하려면 커널화된 SVM 모델을 사용할 수 있다.
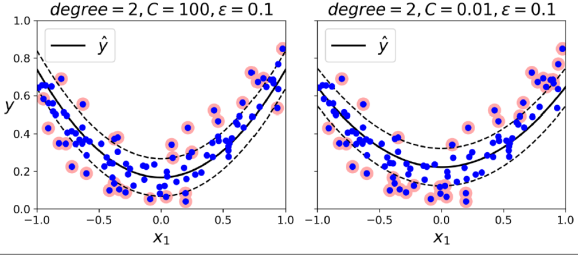
from sklearn. import SVR
svm_poly_reg = SVR(kernel = "poly", degree = 2, C = 100, epsilon = 0.1)
svm_poly_reg.fit(X, y)Under the Hood
Decision Function and Predictions
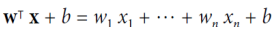

선형 SVM 분류기의 결정 함수는 다음과 같습니다. 결과가 양수이면 예측된 클래스 𝑦^은 양수 클래스(1)이고, 그렇지 않으면 음수 클래스(0)이다.

결정 경계(실선)는 결정 함수가 0과 같은 지점의 집합이다. 점선은 결정 함수가 1 또는 -1과 같은 지점을 나타낸다. 이 점선들은 결정 경계 주위에 평행하며 동일한 거리에 있다. 선형 SVM 분류기를 훈련시키는 것은 마진 위반(hard margin)을 피하거나 이를 제한(soft margin)하면서 이 마진을 가능한 한 넓게 만드는 𝐰 및 𝑏의 값을 찾는 것을 의미한다.
Training Objective
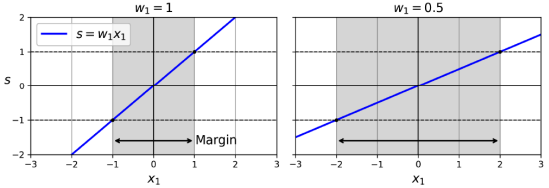
이 모델의 훈련 목표는 먼저 가중치 벡터 𝐰를 최소화하여 가능한 큰 마진을 얻는 것이다. 이를 위해 모든 양수 훈련 인스턴스에 대해 결정 함수가 1보다 크고 음수 훈련 인스턴스에 대해 -1보다 작도록 하는 제약 조건을 도입한다. 이렇게 하면 마진 위반을 피할 수 있다. 하드 마진 선형 SVM 분류기의 목적은 제약이 있는 최적화 문제로 표현되며, 미분 가능한 함수를 최소화하여 마진을 최대화한다. 또한 각 인스턴스에 대해 슬랙 변수를 도입하여 마진 위반을 제어하며, 이를 가능한 작게 유지하여 마진을 크게 만드는 것과의 균형을 맞추기 위해 C 하이퍼파라미터를 사용한다.
Quadratic Programming
Quadratic Programming (QP)은 제한 조건이 있는 이차형식의 목적 함수를 최소화 또는 최대화하는 문제를 다루는 수학적 최적화 기법이다. 일반적인 형태의 QP 문제는 다음과 같다.

여기서 x는 최적화하려는 변수, P는 대칭 행렬, f는 선형 벡터, A는 주어진 행렬, b는 주어진 벡터이다. 이러한 형태의 문제는 제약 조건이 있는 이차형식의 목적 함수를 최적화하는 다양한 실제 세계 문제에서 발견된다.
일반적으로 QP 문제는 행렬 P가 양의 준정치인 경우 또는 제한 조건이 선형적이며 P가 양의 준정치라면 convex 문제로 간주된다. QP 문제는 다양한 응용 분야에서 사용되며, 이를 해결하기 위해 내부적으로 사용되는 다양한 수치 해결 방법이 있다.
The Dual Problem
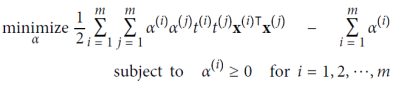
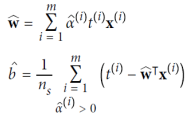
듀얼 문제(The Dual Problem)란, 원래의 문제인 프라이멀 문제(primal problem)와 밀접한 관련이 있는 다른 형태의 제한 조건 최적화 문제이다. 특히, 목적 함수가 볼록이고 부등식 제약 조건이 연속적으로 미분 가능하고 볼록한 함수일 때 충족될 때, 듀얼 문제는 프라이멀 문제와 동일한 해를 가질 수 있다. 운좋게도 SVM 문제는 이러한 조건을 만족하므로 프라이멀 문제나 듀얼 문제 중 선택하여 해를 구할 수 있다. 선형 SVM 문제의 듀얼 형태는 위 식과 같다. 이 식을 최소화하는 벡터 𝛂를 찾으면 프라이멀 문제를 최소화하는 벡터 𝐰와 𝑏를 계산할 수 있다. 듀얼 문제는 커널 트릭을 가능하게 하며 프라이멀 문제는 그렇지 않다.
Kernelized SVMs

커널화된 SVM은 두 차원의 훈련 세트(예: moons 훈련 세트)에 두 번째 차원 다항 변환을 적용한 다음 변환된 훈련 세트에서 선형 SVM 분류기를 훈련시키려고 한다고 가정해보자. 변환된 벡터가 2D가 아닌 3D임을 알 수 있다. 이제 이 두 개의 2D 벡터 a와 b에 대해 이 두 번째 차원 다항 매핑을 적용한 후 변환된 벡터의 내적을 계산해 보자.
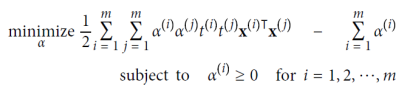
변환된 벡터의 내적은 원래 벡터의 내적의 제곱과 같다.(𝜙(𝐚)𝑇𝜙(𝐛) = (𝐚𝑇𝐛)²) 이것이 SVM의 커널 트릭의 핵심 통찰력이다. 모든 훈련 인스턴스에 변환 𝜙을 적용하면 듀얼 문제에는 𝜙(𝐱(𝑖))𝑇𝜙(𝐱(𝑗))의 내적이 포함된다. 그러나 𝜙가 두 번째 차원 다항 변환인 경우 변환된 벡터의 이 내적을 𝐱(𝑖)𝑇𝐱(𝑗)²로 간단히 대체할 수 있다. 따라서 훈련 인스턴스를 전혀 변환할 필요가 없으며, 단순히 내적을 해당 내적의 제곱으로 대체하면 된다. 함수 𝐾(𝐚, 𝐛) = (𝐚𝑇𝐛)²는 두 번째 차원 다항 커널이다. 머신러닝에서 커널은 변환 𝜙을 계산하지 않고 원래 벡터 𝐚와 𝐛만으로 내적 𝜙(𝐚)𝑇𝜙(𝐛)을 계산할 수 있는 함수이다.
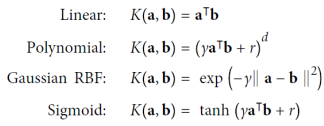
Online SVMs
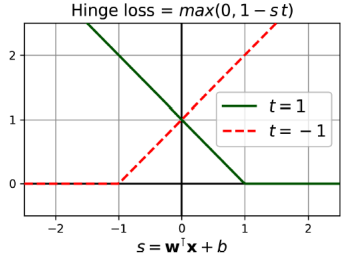
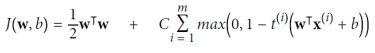
온라인 SVM은 선형 SVM 분류기의 경우 다음 비용 함수를 최소화하기 위해 경사 하강법을 사용하는 한 가지 방법이다. 이 비용 함수는 프라이멀 문제(primal problem)에서 유도된다. 안타깝게도, 경사 하강법은 QP에 기반한 방법보다 수렴 속도가 훨씬 느리다. 비용 함수의 첫 번째 합은 모델이 작은 가중 벡터 w를 가져야 하도록 만들어 더 큰 여유를 확보한다. 두 번째 합은 모든 여유 위반의 총합을 계산한다. 인스턴스의 여유 위반은 거리에 비례하며 거리가 거리의 올바른 측면에 위치한 경우 0이 된다. 두 번째 항을 최소화하면 모델이 여유 위반을 최소화하도록 보장할 수 있다. max(0, 1 - st) 함수를 힌지 손실 함수라고 한다.
주섬주섬
skict-learn을 사용하면 수식이나 이론을 상세히 알 필요 없이 사용할 수 있으나, svm에 대해 간략한 설명은 under the hood로 설명해놨다.
'컴퓨터공학 > AI' 카테고리의 다른 글
| 기계 학습 7. Ensemble Learning and Random Forests (1) | 2023.10.20 |
|---|---|
| 기계 학습 6. 의사 결정 트리(Decision Trees) (1) | 2023.10.19 |
| 기계 학습 4. 회귀(Regression) 분석 (1) | 2023.10.19 |
| 기계 학습 3. 분류(Classification) (0) | 2023.09.20 |
| 기계 학습 2.프로젝트 진행 과정 (0) | 2023.09.18 |




댓글