서론
다층신경망(Multi-layer Neural Networks)은 인공지능(AI)과 머신러닝에서 사용되는 핵심적인 알고리즘 중 하나로, 복잡한 데이터 문제를 해결할 수 있는 강력한 도구이다. 다층신경망은 그 구조상 복잡한 비선형 관계와 패턴을 모델링할 수 있으며, 이미지 인식, 음성 인식, 자연어 처리 등 다양한 분야에서 뛰어난 성능을 발휘한다. 은닉층의 깊이와 넓이를 조정함으로써, 모델의 성능을 높일 수 있는 가능성이 크며, 현대 AI 기술의 발전에 큰 기여를 하고 있다.
다층신경망
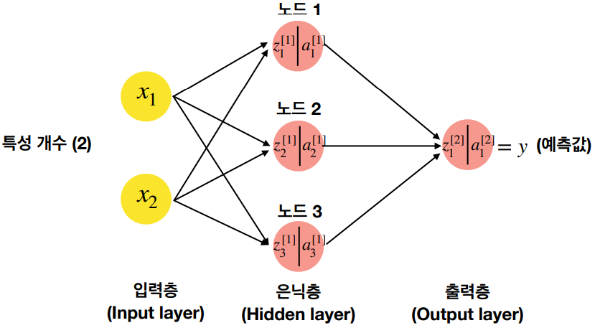


다층신경망(Multi-layer Neural Networks)은 입력층(Input Layer), 하나 이상의 은닉층(Hidden Layers), 그리고 출력층(Output Layer)으로 구성된 신경망 구조를 가지고 있다. 각 층은 노드(또는 뉴런)로 구성되어 있으며, 이 노드들은 서로 가중치(Weight)를 통해 연결되어 있다. 데이터가 신경망을 통과하면서 각 노드에서는 가중치가 적용되고, 활성화 함수(Activation Function)를 통해 다음 층으로 전달되는 값을 결정한다.
핵심 구성 요소
- 입력층(Input Layer): 데이터를 신경망에 입력하는 부분이다. 각 입력 노드는 데이터의 한 특성(feature)을 나타낸다.
- 은닉층(Hidden Layers): 입력층과 출력층 사이에 존재하는 층이다. 다층신경망은 적어도 하나 이상의 은닉층을 가지고 있으며, 이 층들이 신경망이 복잡한 특성과 패턴을 학습할 수 있게 한다. 은닉층의 뉴런 수와 층의 수는 모델의 복잡성과 성능에 영향을 미친다.
- 출력층(Output Layer): 신경망의 최종 예측이나 분류 결과를 출력하는 층이다. 출력 노드의 수는 주로 해결하고자 하는 문제의 유형(예: 분류 클래스의 수)에 따라 결정된다.
은닉층의 중요성
은닉층은 입력층과 출력층 사이에서 중요한 역할을 한다. 은닉층을 통해 다층신경망은 비선형 문제 해결 능력을 갖추게 된다. 은닉층의 뉴런들은 다양한 가중치와 활성화 함수를 통해 복잡한 특성과 패턴을 학습할 수 있으며, 신경망의 깊이와 넓이에 따라 모델의 능력이 달라진다. 이를 바탕으로 더 정확한 예측과 분류를 수행할 수 있다.
은닉층의 활성화 함수
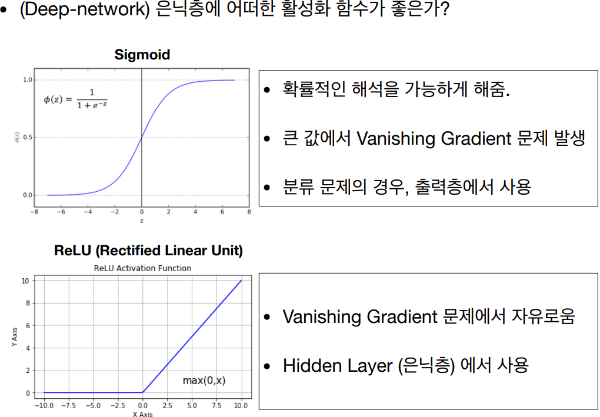
은닉층에서 사용할 활성화 함수의 선택은 주로 해결하고자 하는 문제의 유형과 신경망의 구조에 따라 달라진다. 여러 활성화 함수가 있지만, 가장 일반적으로 사용되는 몇 가지 활성화 함수에 대해 살펴보자.
ReLU (Rectified Linear Unit)
- 정의: ReLU 함수는 `f(x) = max(0, x)`로 정의된다. 즉, 입력이 0보다 크면 그 입력을 그대로 출력하고, 0 이하면 0을 출력한다.
- 장점: 비선형성을 도입하면서도 계산이 간단하고, 그래디언트 소실 문제(Vanishing Gradient Problem)를 어느 정도 완화해 준다.
- 사용처: 현재 가장 널리 사용되는 활성화 함수 중 하나로, 일반적인 딥러닝 모델에서 좋은 성능을 보인다.
Sigmoid
- 정의: `f(x) = 1 / (1 + exp(-x))`로, 출력 범위가 0과 1 사이이다.
- 장점: 출력이 0과 1 사이로 제한되므로, 확률을 나타내는 데 적합하다.
- 단점: 깊은 네트워크에서 그래디언트 소실 문제를 야기할 수 있다.
- 사용처: 이진 분류 문제의 출력층에서 주로 사용된다.
Tanh (Hyperbolic Tangent)
- 정의: `f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))`로, 출력 범위가 -1과 1 사이이다.
- 장점: Sigmoid 함수와 비슷하지만, 출력 범위가 -1과 1 사이이므로, 중심이 0에 가까워 학습 초기 단계에서 빠르게 수렴할 수 있다.
- 단점: 깊은 네트워크에서 그래디언트 소실 문제를 겪을 수 있다.
- 사용처: 순환 신경망(RNN)과 같은 특정 모델에서 선호된다.
Leaky ReLU
- 정의: Leaky ReLU는 `f(x) = x if x > 0 else alpha * x`로, `alpha`는 작은 상수이다. 이는 음수 입력에 대해 완전히 0이 아닌 작은 기울기를 제공한다.
- 장점: ReLU의 죽은 뉴런 문제(Dead Neurons Problem)를 어느 정도 해결해 준다.
- 사용처: ReLU를 사용할 때 나타날 수 있는 일부 문제를 방지하고자 할 때 유용한다.
선택 가이드
일반적으로 ReLU 함수가 가장 널리 사용되며, 대부분의 경우 좋은 성능을 보인다. 그러나 ReLU가 일부 뉴런을 "죽게" 만들 수 있는 문제를 해결하기 위해 Leaky ReLU나 다른 변형을 사용할 수 있다. 만약 문제가 이진 분류의 경우 출력층에서 Sigmoid를 사용한다. 신경망이 깊어지면 Tanh나 Sigmoid 함수의 그래디언트 소실 문제를 고려해야 한다.
결국, 사용할 활성화 함수는 문제의 유형, 네트워크 구조, 그리고 실험을 통해 결정하는 것이 좋다.
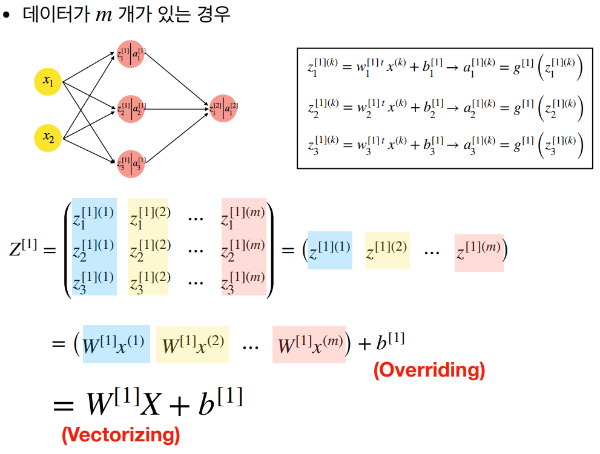
데이터 처리
신경망에서의 계산은 주로 벡터와 행렬 연산으로 이루어진다. 벡터 연산을 행렬 연산으로 확장함으로써, 복수의 데이터 처리가 동시에 가능해져 계산 효율성이 크게 향상된다. 이는 특히 대규모 데이터셋을 다루는 딥러닝에서 중요한 요소이다.
핵심 원리
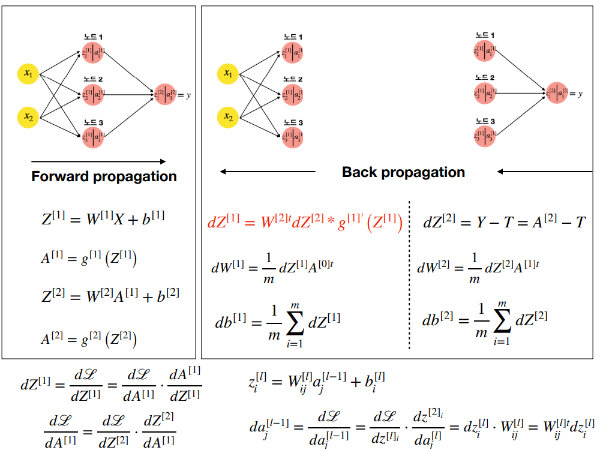
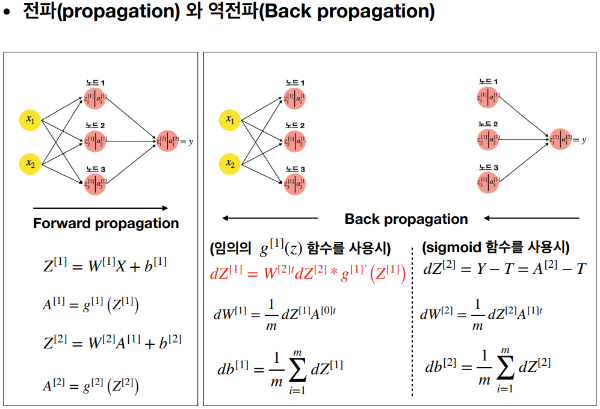
- 전파(Forward Propagation): 입력 데이터가 신경망을 통해 앞으로 전파되면서 각 층의 뉴런에서 가중치와 활성화 함수가 적용되는 과정이다. 이 과정을 통해 최종적으로 출력층에서 예측 결과를 얻는다.
- 역전파(Backpropagation): 네트워크의 예측 결과와 실제 값 사이의 오차를 계산한 후, 이 오차를 사용하여 네트워크의 가중치를 조정하는 과정이다. 이는 신경망이 올바른 예측을 할 수 있도록 학습하는 데 필수적이다.
- 학습률(Learning Rate): 가중치를 업데이트할 때 적용되는 비율로, 학습 속도와 정확도에 영향을 미친다.
학습하기
다층신경망(Multi-layer Neural Network) 학습 과정은 복잡한 데이터에서 패턴을 인식하고 학습하기 위해 설계되었다. 이 과정은 크게 데이터 준비, 순전파(forward propagation), 손실 함수 계산, 역전파(backpropagation), 그리고 가중치 업데이트의 단계로 나눌 수 있다.
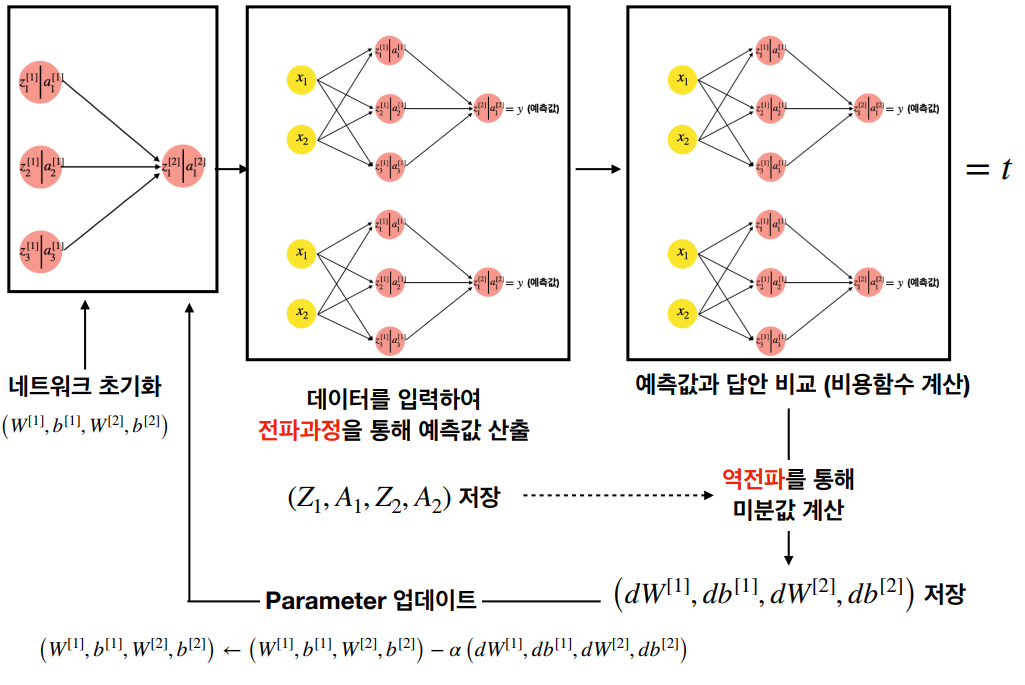
- 데이터 준비
- 학습을 시작하기 전에, 데이터를 수집하고 이를 훈련 세트와 테스트 세트로 나눈다. 데이터는 특성(feature)에 대해 정규화나 표준화를 수행하여 네트워크에 적합한 형태로 가공된다. - 순전파 (Forward Propagation)
- 입력 데이터는 입력층에서부터 시작하여 네트워크의 각 층을 통과한다. 각 층에서는 노드의 가중치와 바이어스를 사용하여 입력 신호의 가중합을 계산하고, 이를 활성화 함수에 통과시켜 다음 층으로 전달한다.
- 이 과정은 출력층까지 반복되며, 최종적으로 예측 결과를 생성한다. - 손실 함수 계산
- 신경망의 예측 결과와 실제 값 사이의 오차를 계산하기 위해 손실 함수(loss function)를 사용한다. 손실 함수는 네트워크의 성능을 수치화하며, 가장 일반적인 예로는 평균 제곱 오차(Mean Squared Error, MSE)와 교차 엔트로피(Cross-Entropy)가 있다.
- 손실 함수의 값은 학습 과정에서 네트워크가 최소화하려고 하는 목표입니다. - 역전파 (Backpropagation)
- 손실 함수의 값에 대한 각 가중치의 기울기(미분값)를 계산하여, 어떻게 가중치를 조정해야 손실을 줄일 수 있는지를 결정한다. 이 과정은 연쇄 법칙(chain rule)을 사용한 미분을 통해 이루어진다.
- 이 기울기는 네트워크를 거슬러 올라가며 계산된다. 즉, 출력층에서부터 시작하여 입력층 방향으로 진행한다. - 가중치 업데이트
- 역전파 과정을 통해 얻은 기울기를 사용하여 네트워크의 가중치를 업데이트한다. 가중치는 일반적으로 경사 하강법(Gradient Descent) 또는 그 변형을 사용하여 업데이트된다.
- 학습률(Learning Rate)은 이 단계에서 가중치를 업데이트할 때 얼마나 큰 단계를 밟을지 결정한다. - 반복
- 이러한 과정을 여러 에포크(epoch)에 걸쳐 반복한다. 각 에포크는 전체 훈련 데이터 세트를 한 번씩 네트워크에 통과시키는 것을 의미한다.
- 네트워크의 성능이 충분히 좋아지거나, 더 이상 개선되지 않을 때까지 학습을 계속한다.
단층신경망(Single-layer Neural Networks)과 비교
단층신경망(Single-layer Neural Networks)과 다층신경망(Multi-layer Neural Networks)은 구조적인 차이가 있으며, 이로 인해 처리할 수 있는 문제의 복잡도에서도 차이가 난다.
단층신경망은 가장 기본적인 형태의 신경망으로, 입력층(Input Layer)과 출력층(Output Layer)만을 포함한다. 즉, "단층"이라는 용어는 은닉층(Hidden Layer)이 없다는 의미이다. 각 입력 노드는 출력 노드에 직접 연결되며, 이 연결에는 가중치(Weight)가 적용된다. 단층신경망은 주로 선형 분류나 회귀 문제에 사용된다.
| 단층신경망 | 다층신경망 |
| 은닉층이 없음 | 하나 이상의 은닉층을 포함 |
| 선형 분류나 선형 회귀 문제에 주로 사용 | 복잡한 비선형 문제를 해결할 수 있는 능력 |
| 복잡한 문제를 해결하기에는 제한적인 능력 | 깊은 학습과 고차원적인 데이터 처리에 적합 |
차이점 요약
- 구조: 단층신경망은 은닉층이 없으며, 다층신경망은 하나 이상의 은닉층을 포함한다.
- 문제 해결 능력: 단층신경망은 주로 간단한 선형 문제에 사용되며, 다층신경망은 복잡한 비선형 문제를 해결할 수 있다.
- 용도: 단층신경망은 선형 분류나 회귀에 주로 적합하고, 다층신경망은 이미지 인식, 음성 인식, 자연어 처리 등의 복잡한 문제에 적합하다.
이러한 차이점으로 인해, 단층신경망과 다층신경망은 각각의 특정 문제에 대해 서로 다른 성능을 보인다. 복잡한 문제를 해결하고자 할 때는 다층신경망이 더 적합한 선택이 된다.
단층 네트워크와 다른 점: 가중치 초기화 문제
단층 신경망(Single-layer Neural Network)과 다층 신경망(Multi-layer Neural Network) 사이에서 가중치 초기화는 중요한 차이점 중 하나이다. 네트워크의 성능과 학습 속도에 큰 영향을 미칠 수 있는데, 이는 신경망의 깊이가 증가함에 따라 더욱 복잡해진다.
단층 신경망에서의 가중치 초기화
단층 신경망에서는 입력층과 출력층만 존재한다. 여기서 가중치 초기화는 상대적으로 간단하다. 초기 가중치는 네트워크 학습을 시작할 때 무작위로 설정되며, 이 초기값은 학습 과정에서 점차 조정된다. 초기 가중치를 무작위로 설정하는 주된 이유는 대칭성을 깨뜨리기 위해서이다. 모든 가중치가 같은 값으로 시작한다면, 모든 노드가 동일한 방식으로 업데이트되어 학습이 제대로 이루어지지 않는다.
다층 신경망에서의 가중치 초기화
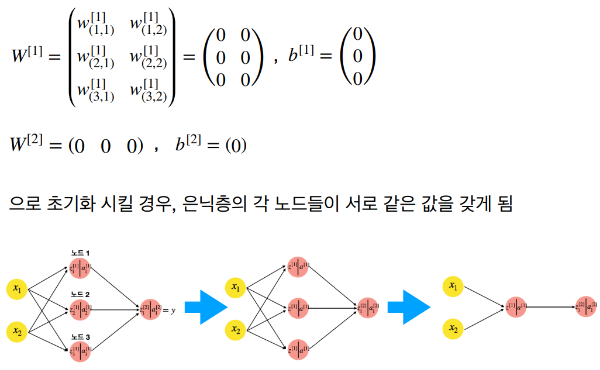
다층 신경망에서 가중치 초기화는 더 복잡하고 중요한 문제가 된다. 다층 구조에서는 적절한 초기 가중치가 학습의 효율성과 최종 성능에 큰 영향을 미친다. 특히, 깊은 네트워크에서는 초기 가중치가 너무 크거나 작으면 그래디언트 소실(Vanishing Gradient) 또는 그래디언트 폭발(Exploding Gradient) 문제가 발생할 수 있다.
- 그래디언트 소실: 가중치가 너무 작게 초기화되면, 네트워크가 깊어질수록 그래디언트가 점점 작아져서 가중치 업데이트가 제대로 이루어지지 않는 현상이다.
- 그래디언트 폭발: 반대로 가중치가 너무 크게 초기화되면, 그래디언트가 점점 커져서 학습이 불안정해지는 현상이다.
이러한 문제를 해결하기 위해 다양한 가중치 초기화 기법이 제안되었다. 예를 들어, Xavier 초기화(Glorot 초기화)와 He 초기화는 가중치를 네트워크의 층 크기에 따라 조정하여 초기화함으로써, 깊은 네트워크에서 그래디언트 소실이나 폭발 문제를 줄이는 데 도움이 된다.
참고
shallow pre
import numpy as np # 넘파이 부르기
import matplotlib.pyplot as plt # 플롯 패키지 부르기
N = 300 # number of points per class
D = 2 # dimensionality
K = 2 # number of classes
x = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
ix = range(N*j,N*(j+1))
r = np.linspace(0.0,1,N) # radius
t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
x[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
y[ix] = j
# lets visualize the data:
plt.scatter(x[:, 0], x[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()
X=x.T
T=(np.array([y]))
print("[X]=",X.shape, ' [T]=', T.shape)# 각 레이어의 가중치와 편향을 초기화 함
def initialize_parameters(n_x, n_h, n_t):
"""
함수 인자:
n_x -- 인풋 레이어 노드 수
n_h -- 히든 레이어 노드 수
n_t -- 결과 레이어 노드 수
리턴값:
params -- 딕셔너리 형태로 값 전달:
[W1] = (n_h, n_x)
[b1] = (n_h, 1)
[W2] = (n_t, n_h)
[b2] = (n_t, 1)
"""
# 가중치는 평균 0을 근처로 deviation =0.01 (sigma^2 = 0.0001) 의 Normal distribution
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_t,n_h)*0.01
b2 = np.zeros((n_t,1))
parameters = {"W1": W1,"b1": b1,"W2": W2, "b2": b2}
return parameters
활성화 함수를 정의: 1) tanh 2) sigmoid 3) ReLu
def activation(X, func):
if func=='tanh' :
A = np.tanh(X)
elif func=='sigmoid' :
A = 1/(1+np.exp(-X))
elif func=='relu' :
A = np.maximum(0,X)
else :
print('Activation function is not well defied')
end() # Activation 이 제대로 정의가 안되면, 함수를 종료함.
return A
# 전파 함수 : 데이터를 넣어서 최종 결과를 출력
def forward_propagation(X, parameters,func):
"""
함수 인자:
[X] = (n_x, m) 여기서 m= 데이터 갯수
parameters = 가중치와 편향들을 받음.
리턴값:
A2 -- 아웃풋 레이어 결과 값
cache -- 각 노드들의 선형 결과값과 activation 함수 결과 값
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
Z1 = np.dot(W1,X)+b1
A1= activation(Z1, func)
Z2 = np.dot(W2,A1)+b2
A2 = activation(Z2,'sigmoid') # 아웃풋 레이어의 activation 함수는 sigmoid 를 줌
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1, "A1": A1,"Z2": Z2,"A2": A2}
return A2, cache
# 비용 함수 정의
def compute_cost(A2, T):
"""
크로스 엔트로피로 계산한 손실함수를 전부 합하여, 비용함수 계산.
함수 인자:
A2 -- 아웃풋 레이어의 결과 값, [A2]= (1,m)
T -- 레이블 , [T]= (1,m)
리턴값:
cost -- 이진분류용 크로스엔트로피를 더한 비용함수.
"""
m = T.shape[1] # 데이터 갯수
delta = 0.0001 # 로그함수안에 log(0)을 방지하기 위한 작은 수
loss = -(np.multiply(T,np.log(A2+(A2==0)*delta))+np.multiply((1-T),np.log(1-A2+(A2==1)*delta))) # 크로스 엔트로피 계산
cost = np.sum(loss)/m # 비용함수
cost = float(np.squeeze(cost)) # 스칼라 양으로 받음.
return cost
# 역전파 함수를 계산하기 위해, activation 함수의 미분함수 계산
def back_activation(X, A, func):
if func == 'tanh' :
dX = 1-np.power(A,2)
elif func == 'sigmoid' :
dX = np.multiply((1-A),A)
elif func == 'relu' :
dX = (X>0)*1.0
return dX
# 역전파
def backward_propagation(parameters, cache, X, T,func):
"""
함수 인자:
parameters -- 각 노드간의 가중치와 편향
cache -- 각 노드의 선형인자와 활성화 인자의 저장소. "Z1", "A1", "Z2", "A2".
X -- 데이터
T -- 지도학습을 위한 레이블
리턴값:
grads -- 가중치 및 편향의 미분값.
"""
m = X.shape[1]
W1 = parameters['W1']
W2 = parameters['W2']
Z1 = cache['Z1']
A1 = cache['A1']
Z2 = cache['Z2']
A2 = cache['A2']
# 역전파 계산을 통한 그래디언트 계산 dW1, db1, dW2, db2.
dZ2 = A2 - T
dW2 = np.dot(dZ2, A1.T)/m
db2 = np.sum(dZ2,axis=1, keepdims=True)/m
dZ1 = np.multiply(np.dot(W2.T,dZ2),back_activation(Z1, A1, func))
dW1 = np.dot(dZ1,X.T)/m
db1 = np.sum(dZ1,axis=1, keepdims=True)/m
grads = {"dW1": dW1, "db1": db1,"dW2": dW2, "db2": db2}
return grads
# 역전파를 통하여, 가중치와 편향을 업데이터 함: Gradient Descent 방식을 사용
def update_parameters(parameters, grads, learning_rate = 1.2):
"""
역전파를 계산을 통해 가중치와 편향을 업데이트 함.
함수 인자:
parameters -- 각 노드간의 가중치와 편향
grads -- 가중치 및 편향의 미분값.
리턴값:
parameters -- 역전파를 통해 업데이트된 각 노드간의 가중치와 편향
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
W1 = W1 - learning_rate* dW1
b1 = b1 - learning_rate*db1
W2 = W2 - learning_rate*dW2
b2 = b2 - learning_rate*db2
parameters = {"W1": W1,"b1": b1, "W2": W2, "b2": b2}
return parameters
# 초기화, 전파, 역전파, 업데이트 부분들을 조합하여, 학습 네트워크 구성
def model(X, T, n_h, func,num_iterations = 10000, print_cost=False):
"""
함수 인자:
X -- 데이터
T -- 데이터에 대한 레이블 값. (지도학습시 사용)
n_h -- 은닉층 (히든 레이어)의 노드 개수
num_iterations -- 그레디언트 디센트 방법의 반복 횟수
print_cost -- 비용함수를 1000번 반복당 출력할지에 대한 여부.
리턴값:
parameters -- 각 노드간의 가중치와 편향. 최종적으로 예측을 할 때 사용됨.
"""
np.random.seed(3)
n_x = X.shape[0]
n_t = T.shape[0]
# 가중치 및 편향의 초기화
parameters = initialize_parameters(n_x, n_h, n_t)
# 그레디언트-디센트 방식을 통해 반복 학습.
for i in range(0, num_iterations):
# 전파, 함수인자= 데이터, 파라메터, 은닉층 활성화 함수 타입, 리턴값 = 최종 아웃풋 값, 캐시 (각 노드의 선형인자와 활성화인자값).
A2, cache = forward_propagation(X, parameters,func)
# 비용함수 계산
cost = compute_cost(A2, T)
# 역전파 . 함수인자= 파라메터, 캐시, 데이터, 레이블 값, 은닉층 활성화 함수 타입 . 리턴값= 그레디언트
grads = backward_propagation(parameters, cache, X, T,func)
# 파라메터 없데이트. 함수인자= 파라메터, 그레디언트, 학습율,리턴값 = 파라메터
parameters = update_parameters(parameters, grads, learning_rate = 1.2)
# 1000번당 비용함수 출력
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
def predict(parameters, X,func):
"""
조율된 파라메터들을 가지고, 데이터의 결과 값 예측
함수인자:
parameters -- 파라메터
X -- 데이터
func -- 학습에 사용된 은닉층의 활성화 함수
리턴값:
예측 -- 색깔 예측 (빨강: 0 / 파랑: 1)
"""
# 확률이 0.5 이상일 경우 파랑색으로 예측
decision_prob = 0.5
A2, cache = forward_propagation(X, parameters,func)
predictions = (A2 > decision_prob)*1.0
return predictionsdef plot_decision_boundary(pred_func,X, y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole gid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
# 활성화 함수 tanh
function='tanh'
nh=4
parameters = model(X, T, nh,func=function,num_iterations = 10000, print_cost=True)
# Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T,func=function), X, y) # 파이썬의 lambda 함수 사용
plt.title("Number of hidden layers= " + str(nh))
# 활성화 함수 relu
function='relu'
plt.figure(figsize=(10, 10))
hidden_layer_sizes = [1, 5, 10, 50]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(2, 2, i+1)
parameters = model(X, T, n_h, func=function,num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T, function), X, y) # Python 의 lambda 함수 사용법
predictions = predict(parameters, X,function)
accuracy = float((np.dot(T,predictions.T) + np.dot(1-T,1-predictions.T))/float(T.size)*100)
accuracy= round(accuracy,1)
plt.title("Accuracy for {} n_h: {} %".format(n_h, accuracy))
# 활성화 함수 tanh
function='tanh'
plt.figure(figsize=(10, 10))
hidden_layer_sizes = [1, 5, 10, 50]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(2, 2, i+1)
parameters = model(X, T, n_h, func=function,num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T, function), X, y) # Python 의 lambda 함수 사용법
predictions = predict(parameters, X,function)
accuracy = float((np.dot(T,predictions.T) + np.dot(1-T,1-predictions.T))/float(T.size)*100)
accuracy= round(accuracy,1)
plt.title("Accuracy for {} n_h: {} %".format(n_h, accuracy))
# 활성화 함수 sigmoid
function='sigmoid'
plt.figure(figsize=(10, 10))
hidden_layer_sizes = [1, 5, 10, 50]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(2, 2, i+1)
parameters = model(X, T, n_h, func=function,num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T, function), X, y) # Python 의 lambda 함수 사용법
predictions = predict(parameters, X,function)
accuracy = float((np.dot(T,predictions.T) + np.dot(1-T,1-predictions.T))/float(T.size)*100)
accuracy= round(accuracy,1)
plt.title("Accuracy for {} n_h: {} %".format(n_h, accuracy))SNN Classification
# mnist에서 손글씨 데이터 추출하기
from tensorflow.keras.datasets import mnist
import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
print(train_images.shape,train_labels.shape)
print(test_images.shape,test_labels.shape)
i=0
import matplotlib.pyplot as plt
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.show()
print(train_labels[i])
j=10
import matplotlib.pyplot as plt
plt.imshow(train_images[j])
plt.show()
print(train_labels[j])# 데이터를 학습에 맞도록 크기를 변환
from tensorflow.keras.utils import to_categorical
train_images=train_images.astype('float32')/255
test_images=test_images.astype('float32')/255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
print(train_labels[i])
print(train_labels[j])
print(train_images.shape)
print(train_labels.shape)
# 학습
from tensorflow.keras import models
from tensorflow.keras import layers
model=models.Sequential()
model.add(layers.Flatten(input_shape=(28,28)))
model.add(layers.Dense(100,activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.summary()# cost function을 최소화 시키는 방법: RMSprop을 사용
from tensorflow.keras import optimizers
#model.compile(optimizers.RMSprop(learning_rate=0.001,rho=0.9),loss='categorical_crossentropy',metrics=['accuracy'])
model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy'])
history1= model.fit(train_images,train_labels,epochs=10, batch_size=100, validation_data=(test_images, test_labels))
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('test accuracy=',test_acc)
history1_dict= history1.history
history1_dict.keys()
history1_dict= history1.history
loss = history1_dict['loss']
val_loss = history1_dict['val_loss']
accuracy = history1_dict['accuracy']
val_accuracy = history1_dict['val_accuracy']
epochs = range(1, len(loss)+1)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.plot(epochs, loss, 'bo',label='training loss')
plt.plot(epochs, val_loss, 'b', label='test loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(122)
plt.plot(epochs, accuracy, 'bo',label='training accuracy')
plt.plot(epochs, val_accuracy, 'b', label='test accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim((0.9,1.02))
plt.legend()
plt.tight_layout()
plt.show()# RMSprop 대신 ADAM optimizer 사용
from tensorflow.keras import optimizers
model=models.Sequential()
model.add(layers.Flatten(input_shape=(28,28)))
model.add(layers.Dense(100,activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
#model.compile(optimizers.Adam(learning_rate=0.001,beta_1=0.9, beta_2= 0.999),loss='categorical_crossentropy',metrics=['accuracy'])
model.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
history2= model.fit(train_images,train_labels,epochs=10, batch_size=100, verbose=2, validation_data=(test_images, test_labels))
history2_dict= history2.history
loss2 = history2_dict['loss']
val_loss2 = history2_dict['val_loss']
accuracy2 = history2_dict['accuracy']
val_accuracy2 = history2_dict['val_accuracy']
epochs2 = range(1, len(loss2)+1)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.plot(epochs, loss, 'ro',label='training loss with RMSprop')
plt.plot(epochs, val_loss, 'r', label='test loss with RMSprop')
plt.plot(epochs, loss2, 'bo',label='training loss with ADAM')
plt.plot(epochs, val_loss2, 'b', label='test loss with ADAM')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(122)
plt.plot(epochs, accuracy, 'ro',label='training accuracy with RMSprop')
plt.plot(epochs, val_accuracy, 'r', label='test accuracy with RMSprop')
plt.plot(epochs, accuracy2, 'bo',label='training accuracy with ADAM')
plt.plot(epochs, val_accuracy2, 'b', label='test accuracy with ADAM')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim((0.9,1.02))
plt.legend()
plt.tight_layout()
plt.show()# Loss function을 Mean Square Error (MSE) 로 하는 경우
model=models.Sequential()
model.add(layers.Flatten(input_shape=(28,28)))
model.add(layers.Dense(100,activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
#model.compile(optimizers.Adam(learning_rate=0.001,beta_1=0.9, beta_2= 0.999),loss='mse',metrics=['accuracy'])
model.compile(optimizer='adam',loss='mse',metrics=['accuracy'])
history3= model.fit(train_images,train_labels,epochs=10, batch_size=100, verbose=2, validation_data=(test_images, test_labels))
history3_dict= history3.history
loss3 = history3_dict['loss']
val_loss3 = history3_dict['val_loss']
accuracy3 = history3_dict['accuracy']
val_accuracy3 = history3_dict['val_accuracy']
epochs3 = range(1, len(loss3)+1)
plt.figure(figsize=(14, 4))
plt.subplot(131)
plt.plot(epochs3, loss2, 'ro',label='training loss with cross entropy')
plt.plot(epochs3, val_loss2, 'r', label='test loss with cross entropy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(132)
plt.plot(epochs3, loss3, 'bo',label='training loss with MSE')
plt.plot(epochs3, val_loss3, 'b', label='test loss with MSE')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(133)
plt.plot(epochs3, accuracy2, 'ro',label='training accuracy with cross entropy')
plt.plot(epochs3, val_accuracy2, 'r', label='test accuracy with cross entropy')
plt.plot(epochs3, accuracy3, 'bo',label='training accuracy with MSE')
plt.plot(epochs3, val_accuracy3, 'b', label='test accuracy with MSE')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim((0.9,1.02))
plt.legend()
plt.tight_layout()
plt.show()인공지능 3. 단층 신경망
서론 단층신경망은 인공지능의 기본이 되는 모델이다. 단층신경망을 통해 기계학습의 기초를 탄탄히 다져보자. 퍼셉트론과 단층신경망 퍼셉트론은 입력층과 출력층, 두 부분으로 구성되어 있
jinger.tistory.com
강화 학습 6.Deep Learning Fundamentals
서론 딥러닝이 발전을 하면서 알파고와 같은 딥러닝과 강화학습이 결합된 형태가 생겨났기에 딥러닝의 간단한 개념에 대해 공부한 다음에 결합된 형태에 대해 알아보자. Artificial Neuron 뉴런은
jinger.tistory.com
'컴퓨터공학 > AI' 카테고리의 다른 글
| 인공지능 6. CNN (0) | 2024.04.25 |
|---|---|
| 인공지능 5. DNN (1) | 2024.04.19 |
| 인공지능 3. 단층 신경망 (1) | 2024.04.07 |
| 인공지능 2. 기초 최적화 이론 (0) | 2024.04.05 |
| 인공지능 1. 퍼셉트론 (0) | 2024.04.01 |




댓글