서론
MDP에서 최적의 정책을 찾기 위해 DP를 사용하였고, DP를 사용하려면 transition과 reward probabilities를 알고 있는 model dynamics에서 가능하였다. 하지만 model dynamics을 모르는 경우도 있을 것이다. 이 경우 환경에 대한 지식이 없을 때 최적의 정책을 찾는 데 매우 강력한 Monte Carlo 알고리즘을 사용한다.
Monte Carlo Methods
Monte Carlo는 반복된 무작위 추출(Sampling)을 이용하여 함수의 값을 수리적으로 근사하는 알고리즘으로 매우 통계적인 방법이다. 이 방법은 물리학과 공학, 컴퓨터 과학 등 다양한 분야에서 가장 인기 있고 가장 일반적으로 사용되는 알고리즘 중 하나이다.
Ex: Estimating the Value of 𝝅 using Monte Carlo
Monte Carlo를 이해하기 쉽게 해주는 예시이다. 아래와 같이 사각형 안에 원의 사분면이 배치되어 있고 사각형 내부에 임의의 점을 생성한다고 할 때, 일부 점은 원 안에 있고 다른 점은 원 밖에 있음을 볼 수 있다.

원안에 있는 점들과 사각형 내부의 점들의 비율은 곧 각 도형의 넓이 간의 비율과 동일하다. 즉, 점들의 비율로 우리는 𝝅를 구할 수 있다.(그림과 같이 4 분할된 원의 넓이는 원의 넓이를 구하는 공식 앞에 1/4을 곱해진다. 아래 식에 이 부분이 생략되어 있다.)



이때 매번 점들이 임의로 정하기에 환경에 따라 𝝅값은 매번 달라지지만, 점들의 양을 늘리면 정확도가 높아진다. 당연히 점들의 양을 무한히 늘리면 더 정확한 𝝅를 구할 수 있다.(이는 적분 개념과 같게 된다.)
import numpy as np
import math
import random
import matplotlib.pyplot as plt
%matplotlib inline
square_size = 1
points_inside_circle = 0
points_inside_square = 0
sample_size = 1000
arc = np.linspace(0, np.pi/2, 100)
#임의의 점을 사각형 크기내에 생성
def generate_points(size):
x = random.random()*size
y = random.random()*size
return (x, y)
#원 내부에 있는 지 확인
def is_in_circle(point, size):
return math.sqrt(point[0]**2 + point[1]**2)<=size
#𝝅값 계산
def compute_pi(points_inside_circle, points_inside_square):
return 4 * (points_inside_circle / points_inside_square)
#점을 찍을 판
plt.axes().set_aspect('equal')
#Monte Carlo Methods
for i in range(sample_size):
point = generate_points(square_size)
plt.plot(point[0], point[1], 'c.')
points_inside_square += 1
if is_in_circle(point, square_size):
points_inside_circle += 1
#모델 출력
plt.plot(1*np.cos(arc), 1*np.sin(arc))
#근사치 출력
print("Approximate value of pi is {}".format(compute_pi(points_inside_circle, points_inside_square)))이런 식으로 매번 불규칙적인 환경에서 샘플을 추출해 통계적으로 문제를 해결하는 것이 Monte Carlo 알고리즘이다.
Monte Carlo Prediction
Monte Carlo 방법은 states, actions, rewards의 샘플 시퀀스만 필요하다. Monte Carlo 방법은 에피소드 작업에만 적용된다. Monte Carlo는 어떤 모델도 필요로 하지 않으므로 모델 없는 학습 알고리즘이다.
MDP에서 정책 𝜋가 있는 상태 S에서 기대되는 수익(expected return)으로 정의하여 최적의 가치 함수를 찾았다. Monte Carlo에서는 기대수익률(expected cumulative future discounted reward) 대신에 평균수익률(mean return)을 사용한다. 이는 기대수익률이 불확실성이 큰 환경에서는 실제로 계산하기 어렵기 때문이다. 기대수익률은 불확실성이 있는 상황에서 미래의 모든 가능한 결과를 고려하여 계산된다. 이는 시뮬레이션에서 각 단계에서 다음 가능한 모든 상태를 고려하여 모든 결과를 평균화하여 계산된다. 이는 시뮬레이션의 결과를 적극적으로 활용하면서도 계산량이 매우 크기 때문에 계산이 어렵다. 반면, 평균수익률은 시뮬레이션에서 실제로 생성된 결과에 대한 평균이다. 이는 시뮬레이션의 결과를 적극적으로 활용하면서도 계산량을 크게 줄일 수 있다. 따라서 Monte Carlo Prediction에서는 기대 수익률(expected return) 대신 평균 수익률(mean return)을 취하여 가치 함수를 근사화한다.
이 방식을 이용하여 Monte Carlo Prediction 알고리즘은 평균을 내는 방법에 따라 First visit Monte Carlo와 Every visit Monte Carlo로 두 가지 유형으로 나뉜다.
steps
Monte Carlo Prediction을 사용하여 주어진 정책의 가치 함수를 추정하는 방법은 다음과 같다.
- 먼저 임의의 값을 가치 함수로 초기화한다.
- 반환(return)을 저장하기 위해 반환들(returns)이라는 빈 목록을 초기화한다.
- 에피소드의 각 상태에 대해 반환(return)을 계산한다.
- 다음으로 수익들 목록에 반환을 추가한다.
- 마지막으로 평균 수익률을 가치 함수로 사용한다.

First Visit Monte Carlo Prediction(first-visit MC prediction)
정책 𝜋에 따라 상태 𝑠의 값인 𝑉𝜋(𝑠)를 추정하고 싶다고 하자. 각 에피소드에서 상태 𝑠의 각 발생을 𝑠의 visit이라고 한다. 물론 𝑠는 같은 에피소드를 여러 번 방문할 수 있다. 이때 여러 번 방문한 같은 s를 평균을 구할 때 사용할 것인가 말 것인가로 방법이 나뉜다.
first-visit MC prediction은 오직 첫 방문(first-vist) 한 상태 s로 평균수익률을 𝑉𝜋(𝑠)로 추정한다. 만약 나중에 같은 s에 방문을 한다면 나중에 방문한 s의 수익은 수익들의 포함되지 않는다.

Every Visit Monte Carlo Prediction(every-visit MC Prediction)
every-visit Monte Carlo에서는 에피소드에서 모든 상태 s를 방문할 때마다 평균 수익을 얻는다. 즉, every-visit MC prediction는 에피소드 초반에 발생한 𝑆𝑡 확인하는 것을 제외하면 first-visit MC prediction와 동일하다. 즉, 슈도코드는 빨간색 네모를 제외하고는 모두 동일하다.(빨간색 네모를 지우면 every-visit MC prediction의 슈도코드가 된다.)

Monte Carlo Prediction
Monte Carlo 방법은 쉽게 이해하고 구현할 수 있으며, 수렴성이 보장되는 방법 중 하나이나. 수렴성 보장에 대해 알아보자. 상태 𝑆에 대한 every-visit(또는 first-visit) 횟수가 무한대가 됨에 따라 first-visit MC와 every-visit MC 모두 𝑉𝜋(𝑠)로 수렴된다.
first-visit MC의 경우, 한 번 방문한 상태에서는 그 이후 방문에서는 해당 상태의 가치함수를 업데이트하지 않는다. 따라서 이 경우에는 해당 상태에 대해 하나의 방문에서 얻은 보상에 대해서만 가치함수를 업데이트하게 된다. 이렇게 하나의 방문에서 얻은 보상을 가지고 가치함수를 업데이트하는 경우, 이 보상들은 서로 독립적(standard deviation)이며, 같은 분포(unbiased estimate)를 가진 확률변수들이다. 이에 따라 first-visit MC은 "큰 수의 법칙"(The law of large numbers: 큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다.)에 따라 수렴성이 보장된다.
every-visit MC의 경우, 한 번 방문한 상태에서도 이후에 다시 방문할 수 있다. 따라서 이 경우에는 해당 상태에 대해 여러 방문에서 얻은 보상들의 평균을 가지고 가치함수를 업데이트한다. 이때, 각각의 평균은 역시 독립적이며 같은 분포를 가진 확률변수이다. 이에 따라 every-visit MC도 "큰 수의 법칙"에 따라 수렴성이 보장된다. 따라서, first-visit MC과 every-visit MC은 모두 주어진 상태에서의 가치함수를 학습하는 데 수렴성을 보장한다.
Blackjack
Monte Carlo Prediction을 활용한 대표적인 예시로 블랙잭(Blackjack)이 있다. 이를 구현 및 이해하기 위해 블랙잭의 규칙을 알아야 한다.
※ 게임 규칙:
- 게임의 목표는 모든 카드의 합이 21에 가깝고 21을 초과하지 않는 것이다.
- 카드 J, Q, K의 값은 10이다.
- Ace의 값은 1 또는 11이 될 수 있다.
- 이것은 플레이어의 선택에 따라 다르다.
- 나머지 카드(2~10)의 값은 표시된 숫자와 동일하다.
- 게임은 한 명 또는 여러 명의 플레이어와 한 명의 딜러로 플레이할 수 있다.
- 각 플레이어는 다른 플레이어가 아닌 딜러와만 경쟁한다.
- 처음에는 플레이어에게 두 장의 카드가 주어진다. 이 두 카드는 앞면으로 공개된다. 즉, 다른 사람이 볼 수 있다.
- 딜러에게도 두 장의 카드가 주어진다. 한 장의 카드는 앞면이 공개되지만 다른 카드는 덮은 상태이다. 즉, 딜러는 자신의 카드 중 하나만 보여준다.
- 두 장의 카드를 받은 직후 플레이어나 딜러의 카드 합이 21이면(플레이어가 잭과 에이스를 받았다고 가정하면 10+11=21) 이를 내추럴(natural) 또는 블랙잭(Blackjack)이라고 하며 플레이어나 딜러가 승리한다.
- 두 장의 카드를 받은 직후 딜러의 카드 합이 같으면 무승부이다.
- 각 라운드에서 플레이어는 다른 카드가 필요한지 여부를 결정한다.
- 플레이어의 카드 합이 21을 초과하면 버스트(bust)라고 하여 딜러가 게임에서 이긴다.
- 플레이어에게 카드가 필요한 경우를 히트(hit)라고 하며 플레이어는 플레이어가 원할 때까지 카드를 계속 받을 수 있다.
- 플레이어가 카드가 필요하지 않은 경우 스탠드(stand)라고 하고 딜러의 차례가 된다.
- 딜러는 선택의 여지가 없이 고정된 전략에 따라 히트하거나 스탠드 한다. 딜러는 17 이상의 합계일 경우 스탠드 하고 그렇지 않으면 히트한다.
- 딜러가 파산하면 플레이어가 이긴다. 그렇지 않으면 결과(승리, 무승부)는 최종 합이 21에 가까운 사람에 의해 결정된다.
설명이 부족하다면 아래 참고에 블랙잭 관련 사이트를 참고 바란다.
Blackjack as MDP
블랙잭의 한판은 유한 MDP로 공식화가 가능하다. 블랙잭의 각 게임을 에피소드라 하고 승리, 패배, 무승부에 각각 +1, -1, 0의 보상(Rewards)이 주어진다. 플레이어의 행동은 hit이나 stand 뿐이며 상태는 플레이어의 카드와 딜러의 표시 카드에 따라 다르다.
블랙잭의 신기한 규칙인 에이스 덕분에 플레이어는 에이스의 가치를 결정해야 한다. 플레이어의 카드 합이 10이고 플레이어가 hit을 한 후 에이스를 얻는다면 11로 간주할 수 있다. 그러나 플레이어의 카드 합이 15이고 hit을 후 플레이어가 에이스를 얻는다면, 에이스를 11로 간주하게 된다면 패배하게 된다.
플레이어가 에이스를 가지고 있는 경우 이를 사용 가능한 에이스(usable ace)라고 부른다. 플레이어는 버스트 없이 11로 간주할 수 있다. 플레이어가 에이스를 11로 간주하여 버스트 되면 사용할 수 없는 에이스(nonusable ace)라고 한다. 따라서 플레이어는 세 가지 변수, 즉 현재 합계, 딜러가 보여주는 카드, 사용 가능한 에이스 보유 여부에 따라 결정을 내린다.
First-Visit MC Prediction for Blackjack
first-visit MC를 사용하여 고정 정책(플레이어의 합이 20 또는 21이면 stand, 그렇지 않으면 hit)에 대한 가치 함수 예측을 해보자.
import numpy
import gym
from matplotlib import pyplot
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from collections import defaultdict
from functools import partial
%matplotlib inline
plt.style.use('ggplot')
#환경 세팅
env = gym.make('Blackjack-v0')
env.action_space, env.observation_space
#내가 지정한 정책
def sample_policy(observation):
score, dealer_score, usable_ace = observation
return 0 if score >= 20 else 1
#에픽소드 생성
def generate_episode(policy,env):
#states, action, rewards을 저장할 수 있는 리스트 초기화
states, actions, rewards = [],[],[]
#gym 환경 초기화
observation = env.reset()
while True:
#states 리스트에 state 추가
states.append(observation)
#sample_policy 함수를 사용하여 action을 선택하고 actions 목록에 작업을 추가
action = sample_policy(observation)
actions.append(action)
#sample_policy에 따라 환경에서 작업을 수행하고 다음 상태로 이동하여 보상을 받는다.
observation, reward, done, info = env.step(action)
rewards.append(reward)
#terminal state에서 반복 종료
if done:
break
return states, actions, rewards
#first visit mc prediction 알고리즘
def first_visit_mc_prediction(policy, env, n_episodes):
#빈 값 테이블을 각 상태의 값을 저장하기 위해 초기화
value_table = defaultdict(float)
N = defaultdict(int)
for _ in range(n_episodes):
#다음으로 에피소드를 생성하고 states와 rewards을 저장
states, _, rewards = generate_episode(policy, env)
returns = 0
#각 단계에 대해 rewards을 변수R에 저장하고 S상태를 저장하고 보상의 합계로 수익을 계산
for t in range(len(states) - 1, -1, -1):
R = rewards[t]
S = states[t]
returns += R
#first visit mc를 수행하기 위해 에피소드가 처음 방문되었는지 확인한다.
#처음 방문을 했다면 단순히 returns의 평균을 취하고 상태 값을 returns의 평균으로 지정
if S not in states[:t]: #이 if문이 없다면 every visit mc prediction 알고리즘이다.
N[S] += 1
value_table[S] += (returns - value_table[S]) / N[S]
return value_table
#가치 함수 플로팅
def plot_blackjack(V, ax1, ax2):
player_sum = numpy.arange(12, 21 + 1)
dealer_show = numpy.arange(1, 10 + 1)
usable_ace = numpy.array([False, True])
state_values = numpy.zeros((len(player_sum),len(dealer_show),len(usable_ace)))
for i, player in enumerate(player_sum):
for j, dealer in enumerate(dealer_show):
for k, ace in enumerate(usable_ace):
state_values[i,j,k] = V[player, dealer, ace]
X, Y = numpy.meshgrid(player_sum, dealer_show)
X = numpy.transpose(X)
Y = numpy.transpose(Y)
ax1.plot_wireframe(Y,X,state_values[:,:,0])
ax2.plot_wireframe(Y,X,state_values[:,:,1])
for ax in ax1, ax2:
ax.set_zlim(-1,1)
ax.set_ylabel('player sum')
ax.set_xlabel('dealer showing')
ax.set_zlabel('state-value')
#정의한 함수들 실행
value = first_visit_mc_prediction(sample_policy, env, n_episodes=50000)
value
#승률 분포 보기
fig, axes = pyplot.subplots(nrows=2, figsize=(5,8), subplot_kw={'projection':'3d'})
axes[0].set_title('value function without usable ace')
axes[0].set_title('value function with usable ace')
plot_blackjack(value, axes[0],axes[1])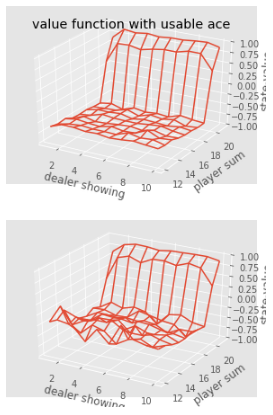
Monte Carlo Control
위에서는 최적의 정책을 고려하지 않았다. 이제 Monte Carlo에서 최적 정책을 찾기 위해 Monte Carlo control를 이용한다. 전반적인 생각은 동적 프로그래밍과 동일한 패턴이다. 즉, 정책 평가와 정책 개선이 상호 작용하는 일반화된 정책 반복(Generalized Policy Iteration, GPI)의 아이디어에 따라 진행한다. 기본적으로 정책 평가와 개선 사이의 루프로 실행된다. 즉, 정책은 항상 가치 함수와 관련하여 개선되고 가치 함수는 정책에 따라 항상 개선된다. 아래 그림에서 evaluation 만 한 게 최적 정책 없이 고정된 정책으로 실행한 것이고, 이번 Monte Carlo control은 평가(evaluation)와 개선(improvement)를 반복하는 것이다.
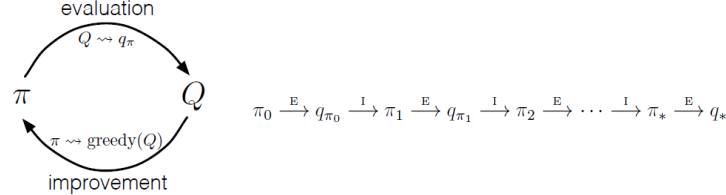
Monte Carlo Exploration Starts(MC-ES)
DP 방법과 달리 여기에서는 상태 값(state values)을 추정하지 않는다. 대신 행동 가치(action values)에 초점을 맞춘다. 환경 모델을 알고 있는 경우 상태 값만으로도 충분하다. 하지만, model dynamics에 대해 모르기 때문에 상태 값만 결정하는 것은 좋은 방법이 아니다. 그렇기에 선택한 정책에 따라 상태 값이 달라지므로 행동 값을 추정하는 것이 상태 값을 추정하는 것보다 직관적이다.
Recall value function and action value function (Q function)
행동 가치를 Q function으로 추정한다. 하지만 여기서 탐색(exploration)의 문제가 발생한다. 해당 상태에 있지 않은 경우 state-action 값에 대해 어떻게 알아야 하며 가능한 모든 actions으로 모든 상태를 탐색하지 않으면 좋은 보상을 놓칠 수 있다는 문제이다.

예를 들어, 블랙잭 게임에서 카드의 합이 20인 상태에 있다고 가정하자. action을 hit만 시도하면 부정적인 보상을 받게 되며, 좋은 상태가 아님을 알게 된다. 그러나 stand action을 시도하면 긍정적인 보상을 받고 실제로 가장 좋은 상태이다. 따라서 우리가 이 특정 상태에 도달할 때마다 우리는 hit 하는 대신 stand 할 수 있다.
어떤 행동이 최선인지 알기 위해서는 각 상태에서 가능한 모든 행동을 탐색하여 최적의 가치를 찾아야 한다. 하지만 모든 행동을 탐색하는 계산은 너무나 방대해질 수 있으며, 불필요한 계산까지 할 수도 있다. 그렇기에 Monte Carlo exploring starts(MC-ES)을 사용한다. MC-ES는 각 에피소드에 대해 초기 상태로 임의의 상태로 시작하고 작업을 수행했다고 가정을 한다. 이렇게 하면 방대한 에피소드를 가능한 모든 actions로 모든 상태를 다룰 수 있다.
steps
- 임의의 값으로 Q function과 policy을 초기화하고 빈 목록으로의 반환도 초기화한다.
- 무작위로 초기화된 정책으로 에피소드를 시작한다.
- 에피소드에서 발생하는 모든 고유한 state-action 쌍에 대한 return을 계산하고 returns 목록에 return을 추가한다.
- 하나의 에피소드에서 동일한 state-action 쌍이 여러 번 발생하고 중복 정보가 있는 점이 없기 때문에 고유한 상태 행동 쌍에 대해서만 반환을 계산한다.
- returns목록을 평균 취하여 해당 값을 Q 함수에 할당한다.
- 해당 상태에 대해 최대 Q(s, a)를 갖는 조치를 욕심 정책(greedy policy)으로 선택하여 상태에 대한 개선된 정책을 찾는다.
이 전체 프로세스를 영원히 또는 많은 에피소드에 대해 반복하여 모든 다른 상태 및 작업 쌍을 다룰 수 있다.

On-policy Monte Carlo Control
Monte Carlo exploration starts에서 모든 상태-행동 쌍을 탐색하고 최댓값을 제공하는 쌍을 선택한다. 그러나 많은 수의 상태와 작업이 있는 상황을 생각해 보면 이는 비현실적인 것을 알 수 있다. MC-ES 알고리즘을 사용하면 상태와 행동의 모든 조합을 탐색하고 가장 좋은 것을 선택하는 데 많은 시간이 걸리기 때문이다. 이를 극복하기 위해 On policy와 Off policy 알고리즘이 있다.
우선, on-policy Monte Carlo Control에서는 𝜖-greedy 정책을 사용한다.
Greedy policy
탐욕 정책(greedy policy)은 탐색된 행동(actions explored) 내에서 최적의 행동(=가장 높은 값을 갖는 것)만을 고르는 정책을 말한다. 하지만 탐색된 행동만을 항상 고른다면 아직 탐색되지 않은 더 좋은 행동을 고르지 못할 수 있다. 이것을 탐색-착취 딜레마(exploration-exploitation dilemma)라고 한다.
𝜖 - greedy policy
그래서 이러한 딜레마를 피하기 위해 𝜖-greedy 정책이라는 새로운 정책을 도입한다. 대부분의 경우 최대 추정 행동 값을 가진 행동을 선택하지만 확률 ε으로 무작위로 행동을 선택한다. 즉, 모든 비탐욕적 행동에는 선택(탐색, exploration)의 최소 확률(𝜖)이 주어지고 나머지 대부분의 확률(1 − 𝜖)은 탐욕적 행동(착취, exploitation)에 주어진다.


Off-policy Monte Carlo Control
"off-policy" 알고리즘은 학습이 대상 정책에서 "떨어진(off)" 데이터로부터 이루어지며 전체 프로세스를 정책에서 벗어난 학습을 하기 위해 사용된다. Off-policy Monte Carlo Control에는 두 가지 정책이 있습니다. 대상 정책(Target policy)과 행동 정책(Behavior policy)이 있다. 대상 정책이란 학습되어 최적의 정책이 되는 정책이고 행동 정책이란 보다 탐구적이고 행동을 생성하는 데 사용되는 정책이다. 행동 정책과 대상 정책은 전혀 관련이 없다. 행동 정책은 가능한 모든 상태와 행동을 탐색하므로 행동 정책은 소프트 정책(soft policy)이지만, 목표 정책(target policy)은 그리디 정책(greedy policy, 최댓값을 가지는 정책을 선택)이다.
On-Policy 방법 - Behavior Policy = Target Policy
Off-Policy 방법 - Behavior Policy ≠ Target Policy
우리의 목표는 대상 정책 𝜋에 대한 Q 함수를 추정하는 것이지만 에이전트는 행동 정책 𝑏라는 완전히 다른 정책을 사용하여 행동한다. 𝑏에서 일어난 공통된 에피소드를 사용하여 𝜋의 가치를 추정할 수 있기 때문이다. 이때 𝜋(𝑎|𝑠) > 0 하면 𝑏(𝑎|𝑠) > 0이 되어야 한다. 이것을 coverage의 가정이라고 한다. 𝑏가 𝜋와 동일하지 않은 상태에서 확률론적이어야 한다는 것은 coverage를 따르기 때문이다. 반면에 𝜋는 action-value function의 현재 추정치와 관련하여 결정론적 욕심 정책일 수 있다. 𝜋는 결정론적 최적 정책이 되는 반면 𝑏는 확률적이고 더 탐색적인 상태로 유지된다.(예: 𝜖-greedy 정책) 이 두 정책 𝜋과 𝑏사이의 공통 에피소드를 중요도 샘플링(Importance sampling)을 통해 추정한다.
중요도 샘플링(Importance sampling)
중요도 샘플링(Importance sampling)은 한 분포에서 다른 분포의 샘플을 사용하여 값을 추정하는 기술이다. 이 중요도 샘플링을 통한 off-policy prediction을 볼 수 있다. 이는 대상와 행동 정책이 고정된 가치를 예측한다는 의미한다. 또한, 이 기술은 보통 중요도 샘플링(Ordinary importance sampling)과 가중 중요도 샘플링(Weighted importance sampling)으로 나뉜다.
Off-policy Prediction via Importance Sampling
Off-policy prediction은 특정 정책을 기반으로 한 에피소드를 사용하여 다른 정책을 평가하는 문제이고 Importance Sampling 기법은 현재 정책에서 생성된 샘플을 이용해 다른 대상 정책의 값들을 추정하는 방법이다.
예를 들어, 현재 정책이 greedy policy이고, 대상 정책이 𝜖-greedy policy인 경우를 생각해보자. 현재 정책으로 생성된 에피소드를 이용하여 대상 정책의 가치함수를 추정하기 위해서는, 각 time step에서의 상태-행동 쌍에 대한 반환값을 대상 정책으로 계산해야 한다. 하지만 현재 정책으로 생성된 에피소드에서는 대상 정책에서 선택하지 않은 상태-행동 쌍이 포함되어 있을 수 있다. 이 경우에는 반환값을 제대로 추정하기 위해서는 이러한 상태-행동 쌍을 포함해야 한다. 이 때, Importance Sampling 기법을 사용하면, 각 상태-행동 쌍에 대한 가중치를 계산하여 이를 이용하여 target policy에서의 반환값을 추정할 수 있다.
상태-행동 쌍 (S, A)에서 target policy에서의 반환값은 다음과 같이 추정된다. 여기서, t는 에피소드의 시간 단계(time step)을 나타내며, π는 대상 정책, b는 현재 정책을 말한다.(여기서 𝑏와 𝜋는 다르며 𝜋와 𝑏 모두 고정되어 주어진다.) 시작 상태 𝑆𝑡가 주어지면 서브시퀀스의 state-action trajectory(𝐴𝑡, 𝑆𝑡+1, 𝐴𝑡+1, …, 𝑆𝑇)는 모든 정책 𝜋에서 발생하는 것이다.(‘Trajectory(궤적)’)
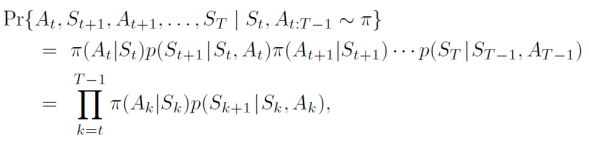
따라서 대상 및 행동 정책(importance-sampling ratio)에 따른 궤적의 상대적 확률은 아래와 같다.
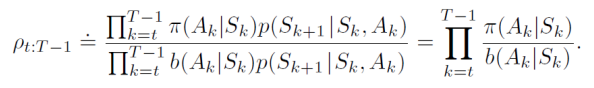
trajectory probabilities은 일반적으로 알려지지 않은 MDP의 transition probabilities에 따라 분자와 분모가 동일하게 나타나 상쇄된다.(서브시퀀스가 정책 𝜋에서 발생했기에 동일) 즉, 중요도 샘플링 비율은 MDP가 아닌 두 정책과 순서에만 의존하게 된다. 이 가중치는 현재 정책과 대상 정책에서 해당 상태-행동 쌍을 선택할 확률의 비율로 계산된다. 따라서 Importance Sampling 기법을 사용하면, 대상 정책에서의 반환값을 현재 정책으로 생성된 에피소드에서 추정할 수 있게 된다.
따라서, Importance Sampling 기법은 현재 policy에서 생성된 에피소드를 이용하여 대상 정책에서의 반환값을 추정하는 방법이다. 이를 이용하여, off-policy prediction 문제를 해결할 수 있다.
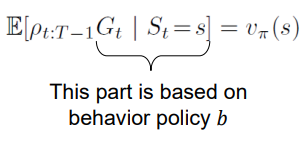
이제 정책 𝑏에 따라 관찰된 에피소드 배치에서 수익을 평균화하는 Monte Carlo 알고리즘으로 𝑣𝜋(𝑠)를 추정해보자.
우리는 상태 𝑠가 방문되는 일련의 시간 단계를 T(s)(로우)로 정의한다. every visit 방법에 대해 상태 𝑠가 방문되는 모든 시간 단계를 포함한다. first visit 방법은 에피소드 내 𝑠에 처음 방문한 시간 단계 포함한다. 에피소드 경계를 넘어 증가하는 방식으로 시간 단계 번호를 지정하는 것이 편리하다. 배치의 첫 번째 에피소드가 시간 100에서 종료 상태로 끝나면 다음 에피소드는 시간 𝑡 = 101에서 시작됩니다. 𝑇(𝑡)는 𝑡 이후 최초 종료 시점을 의미한다. 𝐺𝑡는 𝑡 이후부터 𝑇(𝑡)까지의 return을 의미한다.
𝑣𝜋(𝑠)를 추정하기 위해 단순히 수익률을 비율로 조정하고 결과의 평균을 낸다. 이것은 일반적인 중요도 샘플링이다.

보통 중요도 샘플링(Ordinary importance sampling)
특정 한 에피소드(Trajectory) 내에서 연산을 진행할 때, 분자는 각 상태에 대해 방문한 시점에서의 각각의 반환값과 중요도 비율의 곱을 모두 합한 값이고, 분모는 해당 상태에 방문한 횟수이다. 즉, 이것은 방문 당 해당 상태의 평균의 중요도 비율 값으로서, 가중치된 반환값(비율)을 나타낸다. 따라서, 편향(Bias)되지 않는다. 그러나 분산(Variance)의 측면에서는 비율 값에 대한 분산은 일반적으로 제한이 없기에 분산이 높을 수 있다.

가중 중요도 샘플링(Weighted importance sampling)
모집단에서 표본집단에 대한 평균(weighted average을 사용)을 계산할 때 좀 더 정확한 방식이다. 반환값과의 편차(Biased)는 있지만 변동폭(Variance)이 작다. 그래서 일반적인 케이스에 대해 좀 더 좋은 결과를 보인다.
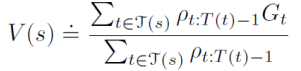
보통 중요도 샘플링(Ordinary importance sampling)과 가중 중요도 샘플링(Weighted importance sampling)의 차이점

이 Monte Carlo 방식이 exploration문제가 있어서 탐색 폴리시와 최종 폴리시를 구분하는 Off-policy 방법이 고안되었다. 그리고 target policy로 얻은 리턴들이 action policy로 이용되려면 ratio 값을 곱해서 평균을 내야 한다. 보통 중요도 샘플링 방법은 말 그대로 평균을 낸 거지만 가중 중요도 샘플링 방법은 직접적인 평균은 아니다.
상태 𝑠에서 single return을 관찰한 후 first-visit 방법의 추정치를 가정한다.
weighted average 추정에서는 단일 수익률에 대한 비율은 분자와 분모에서 상쇄되므로 추정치는 비율과 무관하게 관측된 수익률과 동일하다. 이 수익이 관찰된 유일한 수익이라는 점을 감안할 때 이는 합리적인 추정치이지만 그 기대치는 𝑣𝜋(𝑠)가 아니라 𝑣𝑏(𝑠)이다.
반대로 일반 중요도 샘플링 추정기(Ordinary importance sampling)의 first-visit 버전은 기대에 항상 𝑣𝜋(𝑠)이지만 극단적일 수 있습니다. 비율이 10이라고 가정하면 관찰된 trajectory은 행동 정책에서보다 대상 정책에서 10배 가능성이 있음을 나타낸다. 이 경우 일반적인 중요도 샘플링 추정치는 관찰된 수익의 10배이다. 즉, 에피소드의 trajectory이 대상 정책을 매우 대표하는 것으로 간주되더라도 관찰된 수익과는 상당히 거리가 멀다.
Using weighted importance sampling

Off-policy Monte Carlo Control
에이전트는 대상 정책에 대해 학습하고 개선하면서 행동 정책을 따른다. 이러한 기술은 행동 정책이 대상 정책(coverage)에 의해 선택될 수 있는 모든 행동을 선택할 확률이 0이 아닌 것을 요구한다. 모든 가능성을 탐색하기 위해 행동 정책이 부드러워야(soft) 한다.(즉, 0이 아닌 확률로 모든 상태에서 모든 행동을 선택해야 한다.) 대상 정책 𝜋 ≈ 𝜋∗은 𝑞𝜋의 추정치인 𝑄에 대한 욕심 정책이다. 행동 정책 𝑏은 무엇이든 될 수 있지만 𝜋이 최적의 정책으로 수렴되도록 하려면 각 상태 및 행동 쌍에 대해 무한한 수의 반환을 얻어야 한다. 𝑏를 𝜖-greedy 정책으로 선택하여 보장할 수 있다.
Using weighted-importance sampling
동적 프로그래밍의 일반적인 정책 반복을 기반으로 한다.

주섬주섬
수식들이 매우 보기 싫게 생겼지만, 실제로 직접 값을 대입해보며 이해를 해보는 것이 좋다. 수식과 슈도 코드가 저렇게 된 것은 수학자 및 과학자들이 일반화하기 위한 정리이기에 보기 어려운 것이 당연한 것이다.
논문 "Reinforcement learning with replacing eligibility traces" <Satinder P. Singh & Richard S. Sutton>을 읽어보면 결론적으로 first-visit MC이 every-visit MC보다 일반적으로 좋다. 물론 이는 단편적으로 결론을 지은 것으로 조건들을 따져보면 대체로 비슷하다고도 할 수 있다.
참고
블랙잭 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 블랙잭(영어: Blackjack)은 트웬티원(영어: Twenty-one) 또는 벵테텅(프랑스어: Vingt-et-un)이라고도 하며, 세계의 카지노에서 가장 널리 행해지는 플레잉카드 게임이다.
ko.wikipedia.org
블랙잭(카드게임) - 나무위키
인슈어런스(Insurance) 딜러의 오픈된 카드가 스페이드 A일 경우, 딜러가 블랙잭이 나올 가능성에 대비해 보험을 들어두는 것을 말한다. 건 금액의 절반(절반은 상한일 뿐이고 절반 이하를 지불하
namu.wiki
한국카지노업관광협회
우선 먼저 돈을 테이블 자기 앞에 있는 네모난 곳에 배팅을 하면, 딜러는 두 장의 카드를 숫자가 보이게 나누어 줍니다. 그리고 딜러의 카드는 한 장만 보여 줍니다. 그림카드 K, Q, J 그리고 10은 1
www.koreacasino.or.kr
한국블로그 중에서 잘 정리된 블로그로 만약 제 블로그로 이해가 부족했다면 아래 블로그를 추천한다.
하쿠's 강화학습 :: [Ch. V] Monte Carlo Methods
포스팅에 앞서 이 게시글은 Reference의 contents를 review하는 글임을 밝힌다. 「Monte Carlo Method(몬테카를로 방법)」 이번 포스트의 주제는 'Monte Carlo Method(몬테카를로 방법, 이하 MC)'이다. 앞선 포스트
hakucode.tistory.com
'컴퓨터공학 > AI' 카테고리의 다른 글
| 강화 학습 6.Deep Learning Fundamentals (0) | 2023.05.09 |
|---|---|
| 강화 학습 5.Multi-Armed Bandit (MAB)Problem (0) | 2023.04.25 |
| 강화 학습 4.Temporal Difference(TD) Learning (0) | 2023.04.18 |
| 강화 학습 2. Markov Decision Process(MDP) and Dynamic Programming(DP) (1) | 2023.03.27 |
| 강화 학습 1.기본 개념 (0) | 2023.03.11 |




댓글