서론
Monte Carlo 방법은 에피소드 환경에만 적용된다는 단점과 에피소드가 매우 길면 가치 함수를 계산하기 위해 오랜 시간이 걸린다는 단점이 있다. 따라서 모델 없거나(model-free), 모델 역학(model dynamics)을 미리 알 필요가 없는 비 에피소드 작업에도 적용 가능한 학습 알고리즘인 TD(temporal difference) 학습에 대해 알아보자.
TD(Temporal Difference) Learning
TD방식은 Monte Carlo로 아이디어와 dynamic programming 아이디어의 결합한 방식이다. Monte Carlo 방법과 마찬가지로 TD 방법은 환경의 dynamics models 없이 원시 경험에서 직접 학습할 수 있다. 또한, DP와 마찬가지로 TD 방법은 최종 결과를 기다리지 않고(=에피소드가 끝날 때까지 기다리지 않고) 다른 학습된 추정치를 부분적으로 기반으로 추정치를 업데이트한다. 대신에 이전에 학습된 추정치를 기반으로 현재 추정치를 근사화하는데 이를 부트스트래핑(bootstrapping)라고 한다.
이전 블로그와 마찬가지로 정책 평가 또는 예측 문제(prediction problem), 주어진 정책 𝜋에 대한 가치 함수 𝑣𝜋를 추정하는 문제에 초점을 맞추는 것으로 시작한다. 제어 문제(control problem, 최적 정책 찾기)의 경우 DP, TD 및 Monte Carlo 방법은 모두 일반화된 정책 반복(GPI)의 일부 변형을 사용한다. 방법의 차이는 주로 예측 문제에 대한 접근 방식의 차이가 있다.
Incremental Implementation
강화학습에서 Incremental Implementation은 새로운 환경이나 문제에 대한 적응력을 높이기 위해 에이전트가 경험한 것을 활용하여 지속적으로 개선하는 과정을 말한다. 모델 기반 강화학습에서는 초기에는 모델을 구축하고, 이후에는 모델을 개선해 나가는 과정을 거칩니다. 이를 통해 모델의 정확성을 높이고, 최적의 정책을 학습하는 데에 활용할 수 있다.
예시로 평균 구하는 식의 개선이 있다. 일반적으로 평균은 모든 값을 더하고 값의 수만큼 나눈다. 프로그래밍에서 모든 값을 매번 저장하고 이를 불러와 계산하는 것은 메모리와 처리 시간 측면에서 비효율적이다. 아래와 같은 식을 거쳐 평균은 일정한 메모리와 일정한 시간 단계당 계산을 통해 효율적인 계산 방식으로 계산할 수 있다. 이 구현은 𝑄𝑛 및 𝑛에 대한 메모리만 필요하고 각각의 새로운 보상에 대한 작은 계산만 필요하다.
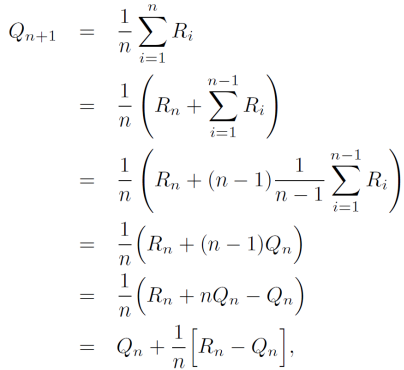
TD Prediction
TD 및 Monte Carlo 방법 모두 경험을 사용하여 예측 문제를 해결한다. 정책 𝜋에 따른 경험이 주어지면 두 방법 모두 해당 경험에서 발생하는 비종료 상태 𝑆𝑡에 대한 𝑣𝜋의 추정치 𝑉를 업데이트한다. Monte Carlo 방법은 방문 후 return이 알려질 때까지 기다린 다음 해당 return을 𝑉(𝑆𝑡)의 대상으로 사용한다. 비정적(nonstationary) 환경에 적합한 간단한 every-visit Monte Carlo 방법은 𝐺𝑡가 시간 𝑡에 따른 실제 반환이고 𝛼가 상수 단계 크기 매개변수이다. 이 방법을 constant - 𝛼 MC라고 부른다.
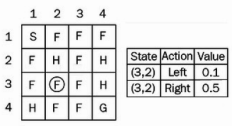
Monte Carlo 방법은 𝑉(𝑆𝑡)의 증분(increment)을 결정하기 위해 에피소드가 끝날 때까지 기다려야 하는 반면(그때에만 𝐺𝑡이 알려짐) TD 방법은 다음 단계까지만 기다리면 된다. 시간 𝑡 − 1에서 그들은 즉시 대상을 형성하고 관찰된 보상 𝑅𝑡+1과 추정치 𝑉(𝑆𝑡+1)을 사용하여 유용한 업데이트를 만든다. 실제로 Monte Carlo 업데이트의 대상은 𝐺𝑡인 반면 TD 업데이트의 대상은 𝑅𝑡+1 + 𝛾𝑉(𝑆𝑡+1)이다. 이 TD 방식은 TD(𝜆)와 n-step TD 방식의 특수한 경우이므로 TD(0) 또는 one-step TD라고 한다.
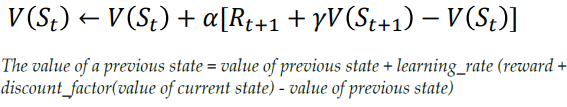
이 식을 직관적으로 생각하면 실제 reward(𝑅𝑡+1 + 𝛾𝑉(𝑆𝑡+1))와 예상 reward(𝑉(𝑆𝑡))의 차이에 learning rate alpha를 곱한 값이다. 이때 학습률(learning rate)은 단계 크기(step size)라고도 불리며 수렴(convergence)에 유용하다. 즉, 실제값과 예측값의 차이를 (𝑅𝑡+1 + 𝛾𝑉(𝑆𝑡+1) − 𝑉(𝑆𝑡))로 취하므로 사실상 오차를 의미하며 TD 오류(TD error, 𝛿𝑡)라고 할 수 있다. 즉, 여러 번의 반복을 통해 이 오류를 최소화하도록 하는 과정이 TD Prediction이다.

Frozen lake examples
얼어붙은 호수 예제로 TD 예측을 이해해 보자.
먼저 𝑉(𝑠)에서 모든 상태에 대해 0으로 값 함수를 0으로 초기화한다.
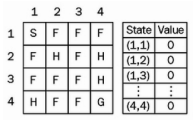
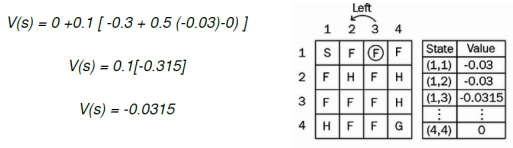
시작 상태(s)(1,1)에 있고 올바른 조치를 취하고 다음 상태(s`)(1,2)로 이동하고 보상(r)을 -0.3으로 받는다고 가정하자.(학습률(𝛼)을 0.1, 할인율(𝛾)을 0.5로 가정)

이제 (1,2)와 같은 상태(s)에 있으므로 올바른 행동을 취하고 (1,3)과 같이 다음 상태(s`)로 이동하고 보상(r) -0.3을 받는다.
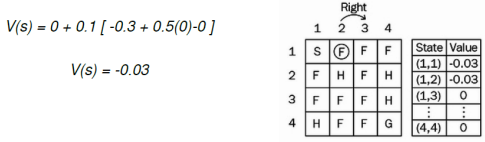
이제 우리는 상태 (s) (1,3)에서 왼쪽으로 조치를 취한다고 가정하자. 다시 상태(s`)(1,2)로 돌아가고 보상(r) -0.3을 받는다.
Advantages of TD Prediction
TD 방법은 부분적으로 다른 추정치를 기반으로 추정치를 업데이트한다. 즉, 추측으로부터 추측을 배운다.(booststarp) TD 방법은 Monte Carlo 및 DP 방법에 비해 어떤 장점이 있을까?
- TD 방법은 다음 상태 전이 확률 분포의 환경 모델이 필요하지 않다는 점에서 DP 방법보다 이점이 있다.
- TD 방법은 온라인에서 완전 증분 방식(fully incremental fashion)으로 자연스럽게 구현된다는 점에서 Monte Carlo 방법보다 이점이 있다.
- Monte Carlo 방법을 사용하면 에피소드가 끝날 때까지 기다린 후에야 반환을 알 수 있다. 반면 TD 방법은 한 단계만 기다리면 된다.
그럼 TD 방법이 타당할까? 확실히 실제 결과를 기다리지 않고 다음 추측에서 하나의 추측을 배우는 것이 편리하지만 여전히 정답에 대한 수렴을 보장할 수 있을지 의문이다. 그러나 모든 고정 정책 𝜋에 대해 TD(0)은 충분히 작은 경우 일정한 단계 크기 매개변수의 평균에서 𝑣𝜋로 수렴하는 것으로 입증되었다.
SARSA: On-policy TD Contro
우리는 일반화된 정책 반복(GPI) 패턴을 따르지만 이번에는 평가 또는 예측 부분에 TD 방법을 사용할 것이다. Monte Carlo 방법과 마찬가지로 우리는 탐색(exploration)과 착취(exploitation)를 절충해야 할 필요가 있다. 접근 방식은 다시 두 가지 주요 클래스인 on-policy과 off-policy으로 나뉩니다.
- Sarsa: on-policy
- Q-learning: off-policy
Sarsa
첫 번째 단계는 상태가치 함수(state-value function)가 아닌 행동가치 함수(action-value function)를 배운다. 특히, on-policy 방법의 경우 현재 동작 정책 𝜋과 모든 상태 𝑠 및 작업 𝑎에 대해 𝑞𝜋(𝑠, 𝑎)를 추정해야 한다. 학습 𝑣𝜋에 대해 이전에 설명한 기본적으로 동일한 TD 방법을 사용하여 수행할 수 있다. 이 업데이트는 비종료 상태(𝑆𝑡)에서 전환할 때마다 수행된다. 𝑆𝑡+1이 종료 상태이면 𝑄(𝑆𝑡+1, 𝐴𝑡+1)은 0으로 정의한다. 여기서 Q value를 업데이트 하기 위해 (𝑆𝑡, 𝐴𝑡, 𝑅𝑡+1, 𝑆𝑡+1, 𝐴𝑡+1)를 사용한다. 모든 on-policy 방법과 마찬가지로 우리는 행동 정책 𝜋에 대한 𝑞𝜋를 지속적으로 추정하고 동시에 𝑞𝜋에 대한 탐욕적(Greedy)으로 𝜋를 변경한다.
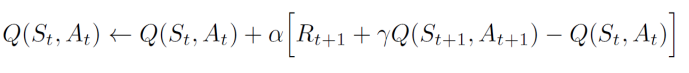

Frozen lake examples
상태(4,2)에 있다고 가정하자. 𝜖-greedy 정책에 따라 조치를 결정하고 확률 1-𝜖을 사용하고 최선의 행동을 선택한다고 가정해 보자.
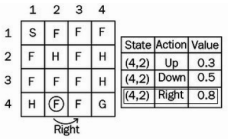
이제 상태 (4,2)에서 바로 작업을 수행한 후 상태 (4,3)에 있다. 이전 상태(4,2)의 값을 어떻게 업데이트될까?
(𝛼 = 0.1, 𝑅𝑡+1 = 0.3, 𝛾 = 1)
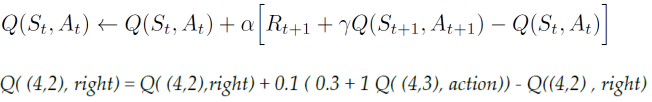
Q((4,3), action)의 값은 𝜖-greedy 정책을 사용하여 선택한다.
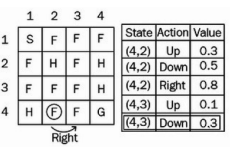
상태 (4,3)에서 Up 및 Down의 두 가지 작업을 탐색했으며 여기에서도 𝜖-greedy 정책을 따른다. 우리는 𝜖 확률로 탐색(explore)하거나 1 − 𝜖 확률로 이용(exploit)한다. 확률 𝜖을 선택하고 새로운 작업을 탐색한다고 가정해 보자.

Solving the taxi problem using SARSA
taxi problem
환경에는 4개의 위치가 있으며 에이전트는 한 위치에서 승객을 태우고 다른 위치에서 내려야 한다. 에이전트는 성공적인 하차에 대한 보상으로 +20 포인트를 받게 되며, 소요되는 모든 단계마다 -1점을 잃는다. 에이전트는 잘못된 승차 및 하차에 대해서도 -10점을 잃는다. 따라서 저희 에이전트의 목표는 불법 승객을 추가하지 않고 단시간에 정확한 위치에서 승객을 태우고 내리는 방법을 배우는 것이다. 문자(R, G, Y, B)는 서로 다른 위치를 나타내며 사각형은 택시를 운전하는 에이전트이다. 아래 환경을 보면 25개의 택시 위치할 수 있고, 5개의 승객 위치 및 4개의 목적지 위치가 있으므로 총 500개의 개별 상태가 있다.
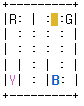
상태 행동에 대한 설명
Passenger locations:
- 1: R(ed)
- 2: G(reen)
- 3: Y(ellow)
- 4: B(lue)
- 5: in taxi
Destinations:
- 1: R(ed)
- 2: G(reen)
- 3: Y(ellow)
- 4: B(lue)
Actions:
- 1: move south
- 2: move north
- 3: move east
- 4: move west
- 5: pick up passenger
- 6: drop off passenger
Rendering:
- blue: passenger
- magenta: destination
- yellow: empty taxi
- green: full taxi
- other letters (R, G, Y and B): locations for passengers and destinations
state space is represented by:
(taxi_row, taxi_col, passenger_location, destination)
구현 코드
import random
import gym
from IPython import display
import time
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
env = gym.make('Taxi-v2')
#taxi problem 환경 구축
env.render()
#Q 테이블에는 상태에서 작업을 수행하는 값을 지정하는 상태-작업 쌍을 저장하는 사전을 초기화한다.
Q = {}
for s in range(env.observation_space.n):
for a in range(env.action_space.n):
Q[(s,a)] = 0.0
#𝜖-greedy policy을 수행하기 위한 함수를 정의
def epsilon_greedy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: Q[state,x])
#필요한 변수를 초기화
#alpha - TD learning rate
#gamma - discount factor
#epsilon - epsilon value in epsilon greedy policy
alpha = 0.4
gamma = 0.999
epsilon = 0.017
#SARSA 알고리즘
for i in range(4000):
#각 에피소드의 누적 보상을 r에 저장
r = 0
#상태 초기화
state = env.reset()
#𝜖-greedy 정책을 사용하여 action 선택
action = epsilon_greedy(state,epsilon)
while True:
#다음 상태에서 작업을 수행하고 다음 상태로 이동
nextstate, reward, done, _ = env.step(action)
#𝜖-greedy 정책을 사용하여 다음 작업을 선택
nextaction = epsilon_greedy(nextstate,epsilon)
#업데이트 규칙을 사용하여 이전 상태의 Q 값을 계산
Q[(state,action)] += alpha * (reward + gamma * Q[(nextstate,nextaction)]-Q[(state,action)])
#다음 작업과 다음 상태로 상태와 작업을 업데이트
action = nextaction
state = nextstate
#보상 저장
r += reward
#에피소드의 최종 상태에 있다면 루프를 나간다.
if done:
break
print("total reward: ", r)
env.close()
#학습이 완료된 후 학습된 Q-table을 사용하여 최적의 정책을 확인
stae = env.reset()
total_reward = 0
while True:
#정책이 최적이기 때문에 탐욕스러운 행동을 선택
action = max(list(range(env.action_space.n)), key = lambda x: Q[state,x])
display.clear_output(wait=True)
display.display(plt.gcf())
env.render()
state, reward, done, _ = env.step(action)
total_reward += reward
print("Episode Reward= ", total_reward)
time.sleep(0.5)
if done:
break
env.close()Q-Learning: Off-policy TD Control
학습된 행동-가치 함수(action-value function) 𝑄는 따르고 있는 정책과 관계없이 최적의 행동-가치 함수 𝑞∗에 직접 근사한다.
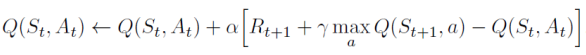

Frozen lake examples
상태(3,2)에 있고 왼쪽과 오른쪽의 두 가지 동작이 있다고 가정해 보자.
우리는 𝜖-greedy 정책을 사용하여 행동을 선택하므로 확률 𝜖을 선택하고 새로운 행동 아래로 탐색하고 새로운 상태(4,2)에 도달한다고 가정하자.
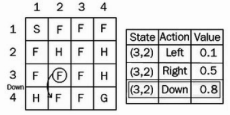
-Q-learning에서 이전 상태(3,2)의 값을 어떻게 업데이트될까? (𝛼 = 0.1, 𝛾 = 1)

Solving the taxi problem using Q-learning
import random
import gym
from IPython import display
import time
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
env = gym.make('Taxi-v2')
#taxi problem 환경 구축
env.render()
#Q 테이블에는 상태에서 작업을 수행하는 값을 지정하는 상태-작업 쌍을 저장하는 사전을 초기화한다.
q = {}
for s in range(env.observation_space.n):
for a in range(env.action_space.n):
q[(s,a)] = 0.0
#Q 학습 업데이트 규칙에 따라 Q 값을 업데이트할 update_q_table이라는 함수를 정의
#아래 함수를 보면 state-action 쌍에 대해 최대값을 갖는 값을 가져와서 qa라는 변수에 저장
#업데이트 규칙에 따라 이전 상태의 Q 값을 업데이트
def update_q_table(prev_state, action, reward, nextstate, alpha, gamma):
qa = max(q[nextstate, a] for a in range(env.action_space.n))
q[(prev_state,action)] += alpha * (reward + gamma *qa - q[(prev_state,action)])
#𝜖-greedy policy을 수행하기 위한 함수를 정의
def epsilon_greedy_policy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: q[state,x])
#필요한 변수를 초기화
#alpha - TD learning rate
#gamma - discount factor
#epsilon - epsilon value in epsilon greedy policy
alpha = 0.4
gamma = 0.999
epsilon = 0.017
#Q Learning 알고리즘
for i in range(8000):
r = 0
state = env.reset()
while True:
#각 상태에서 𝜖-greedy 정책에 따라 행동을 선택
action = epsilon_greedy_policy(state, epsilon)
#action을 수행하고 다음 state로 이동하고 reward를 받는다.
nextstate, reward, done, _ = env.step(action)
#Q 학습 업데이트 규칙에 따라 Q 값을 업데이트하는 update_q_table 함수를 사용하여 Q 값을 업데이트
update_q_table(state, action, reward, nextstate, alpha, gamma)
#이전 상태를 다음 상태로 업데이트
state = nextstate
#획득한 모든 보상 저장
r += reward
#에피소드의 최종 상태에 있다면 루프를 나간다.
if done:
break
print("total reward: ", r)
env.close()
#학습이 완료된 후 학습된 Q-table을 사용하여 최적의 정책을 확인
state = env.reset()
total_reward = 0
while True:
#정책이 최적이기 때문에 탐욕스러운 행동을 선택
action = max(list(range(env.action_space.n)), key = lambda x: q[state,x])
display.clear_output(wait=True)
display.display(plt.gcf())
env.render()
state, reward, done, _ = env.step(action)
total_reward += reward
print('Episode Reward= ', total_reward)
time.sleep(0.5)
if done:
break
env.close()주섬주섬
Monte Carlo 방법을 잘 이해했다면 TD를 이해하는 데 큰 문제가 없다. 단지 에픽소드 끝날 때까지 기다리느냐 아니면 다음 상태까지만 기다리느냐에 차이이다.
참고
강화 학습 2. Markov Decision Process and Dynamic Programming
서론 Markov Decision Process(MDP)는 강화학습에서 문제 정의할 때 많이 사용되는 기법이다. Dynamic Programming는 MDP에서 정의한 수식들을 풀어내기 위한 방법을 말한다. The Markov chain Markov property & Markov chai
jinger.tistory.com
GitHub - openai/gym: A toolkit for developing and comparing reinforcement learning algorithms.
A toolkit for developing and comparing reinforcement learning algorithms. - GitHub - openai/gym: A toolkit for developing and comparing reinforcement learning algorithms.
github.com
'컴퓨터공학 > AI' 카테고리의 다른 글
| 강화 학습 6.Deep Learning Fundamentals (0) | 2023.05.09 |
|---|---|
| 강화 학습 5.Multi-Armed Bandit (MAB)Problem (0) | 2023.04.25 |
| 강화 학습 3.Monte Carlo(MC) Methods (0) | 2023.04.04 |
| 강화 학습 2. Markov Decision Process(MDP) and Dynamic Programming(DP) (1) | 2023.03.27 |
| 강화 학습 1.기본 개념 (0) | 2023.03.11 |




댓글