서론
이전까지는 기초적인 기계학습 알고리즘을 알아보았고 이제 딥러닝에 대해 간략히 알아보자. 인공 신경망(Artificial Neural Networks, ANN)은 생물학적 뉴런 네트워크에서 영감을 받은 기계 학습 모델로, 우리 뇌의 뉴런 구조를 모방하고자 한다. 그러나 시간이 흐름에 따라 ANN은 생물학적 모델과는 상당히 다른 방향으로 발전해왔다. ANN은 딥러닝의 핵심 구성 요소로 자리 잡았으며, 다양하고 강력하며 확장 가능한 특성으로 대규모이고 매우 복잡한 수행을 주로 한다. 이러한 작업에는 거대한 이미지 집합을 분류하는 작업, 음성 인식 서비스를 제공하는 작업, 매일 수백만 명의 사용자에게 가장 적합한 비디오를 추천하는 작업, AlphaGo 등이 있다.
생물학적 뉴런에서 인공 뉴런으로
역사
1943년 신경생리학자 워렌 매컬럭과 수학자 월터 피츠에 의해 처음 소개된 인공 신경망(ANN)은 오랜 시간 동안 존재해왔던 개념이다. 초기의 성공에도 불구하고, 1960년대에는 인공 신경망이 진정으로 지능적인 기계와 대화할 것으로 기대되었으나 이 기대는 실현되지 않아 자금이 다른 분야로 흘러갔고, ANN은 긴 암흑기에 들어갔다. 1980년대 초에는 새로운 아키텍처와 향상된 교육 기술이 등장하여 연결주의(신경망 연구)에 대한 흥미가 다시 살아났으나 1990년대에는 서포트 벡터 머신과 같은 강력한 머신러닝 기술의 등장으로 인해 다시 주목받지 못했다. 그리고 현재는 다시 한 번 ANN의 부흥기가 찾아왔다. 대량의 데이터를 사용하여 ANN을 훈련하는 데 사용할 수 있으며, 매우 크고 복잡한 문제에서 다른 머신러닝 기술을 능가하는 경우가 많아졌다. 또한 1990년대 이후 컴퓨팅 파워(하드웨어)가 크게 증가하면서 큰 신경망을 합리적인 시간에 훈련시킬 수 있게 되었고, 교육 알고리즘의 조정으로 인해 긍정적인 영향을 받았다. ANN은 자금과 진전의 선순환에 들어간 것으로 보인다.
생물학적 뉴런
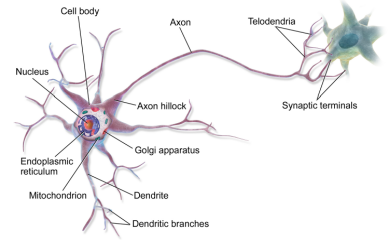
생물학적 뉴런은 액션 포텐셜(action potentials, APs, signals로 불리는 짧은 전기 자극)을 생성하며 이는 축삭을 따라 이동하고 시냅스를 통해 뉴로트랜스미터라 불리는 화학 신호를 방출한다. 뉴런은 몇 밀리초 내에 이러한 뉴로트랜스미터의 충분한 양을 받게 되면 자체적으로 전기 자극을 생성한다. 이러한 간단한 뉴런들의 네트워크를 통해 매우 복잡한 계산이 수행될 수 있다.
뉴런을 이용한 논리적(Logical) 계산

McCulloch과 Pitts는 생물학적 뉴런의 간단한 모델을 제안했는데, 이는 나중에 인공 뉴런으로 알려지게 되었다. 이 모델은 하나 이상의 이진(On/Off) 입력과 하나의 이진 출력을 가지며, 특정 개수 이상의 입력이 활성화되면 출력이 활성화된다. 이러한 인공 뉴런을 사용하여 여러 논리 연산을 수행하는 인공 신경망(ANN)을 만들어보자. 예를 들어, 입력 중 최소 두 개가 활성화되면 뉴런이 활성화되는 경우를 가정하자. 첫 번째 경우 A가 0이면 C에게 0이라는 신호가 두 번 들어가 C도 0이 된다. 반대의 경우도 마찬가지이다. 두 번째 경우 A와 B가 각각 C로 입력하여 겹치는 부분만 C에 출력이 된다. 세번째 경우 A와 B가 각각 C에게 두번 신호를 보내게 되어 A와 B를 모두 포함한 C가 출력이 된다. 네번째 경우 A가 C에게 두 신호를 보내고 B는 자신과 겹치는 부분은 빼도록 신호를 보냈다.
퍼셉트론(The Perceptron)
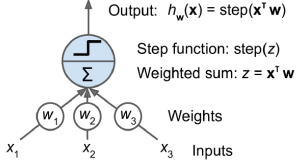
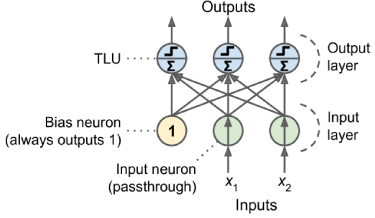

퍼셉트론(Perceptron)은 1957년 Frank Rosenblatt이 고안한 가장 단순한 인공 신경망(ANN) 중 하나이다. 인공 뉴런으로서의 임계 논리 유닛(threshold logic unit, TLU)이나 선형 임계 유닛(linear threshold unit, LTU)과 같은 모델을 기반으로 하며, 주로 헤비사이드 단계 함수나 부호 함수를 계단 함수로 사용한다.
퍼셉트론은 단일 TLU로 이루어진 단일 레이어로 구성되어 간단한 선형 이진 분류에 사용된다. 입력의 선형 조합을 계산하고 그 결과가 임계값을 초과하면 양성 클래스를 출력하고, 그렇지 않으면 음성 클래스를 출력한다. 퍼셉트론은 여러 개의 TLU로 이루어진 단일 레이어로 구성되며, 각 TLU는 모든 입력에 연결된다.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # 꽃잎 길이, 너비
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron()
pre_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5])퍼셉트론의 훈련 알고리즘은 Rosenblatt가 제안한 것으로, Hebb의 법칙에서 영감을 받았다. 퍼셉트론의 훈련은 "함께 활성화되는 세포들은 함께 연결된다"는 원칙에 기초한다.
hw,b(X) = 𝛟 (XW+b)
• 항상 그렇듯이 X는 입력 특성의 매트릭스를 나타낸다. 인스턴스당 하나의 행이 있다. 기능(feature) 당 하나의 열이 있다.
• 가중치 행렬 W에는 편향 뉴런의 연결 가중치를 제외한 모든 연결 가중치가 포함된다. 여기에는 입력 뉴런당 하나의 행과 레이어의 인공 뉴런당 하나의 열이 있다.
• 바이어스 벡터 b에는 바이어스 뉴런과 인공 뉴런 사이의 모든 연결 가중치가 포함된다. 인공 뉴런당 하나의 편향 항을 갖는다.
• 이 함수를 활성화 함수(activation function)라고 한다. 인공 뉴런이 TLUS인 경우 이는 계단 함수(step function)이다.
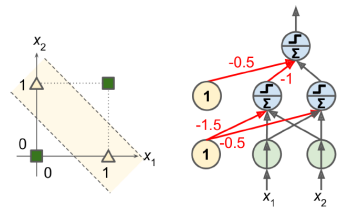
퍼셉트론의 결정 경계는 선형적이므로 복잡한 패턴을 학습할 수 없다는 단점이 있었다. (e.g. XOR 문제) 1969년 Marvin Minsky와 Seymour Papert는 "Perceptrons"에서 이점을 퍼셉트론의 심각한 한계로 지적했다. 그러나 이 한계를 극복하기 위해 여러 개의 퍼셉트론을 쌓아 올린 다층 퍼셉트론(Multilayer Perceptron, MLP)이 등장하였다. MLP는 XOR 문제와 같은 복잡한 패턴을 학습할 수 있어 퍼셉트론의 한계를 극복하였다.
다층 퍼셉트론(MLP)과 역전파(The Multilayer Perceptron and Backpropagation)

다층 퍼셉트론(MLP)은 하나의 입력 레이어, 하나 이상의 은닉 레이어(다층), 그리고 출력 레이어로 구성된다. 신호는 한 방향으로만 흐르며(입력에서 출력으로), 이러한 구조는 피드포워드 신경망(feedforward neural network, FNN)의 한 예로 볼 수 있다. 은닉 레이어가 깊게 쌓인 신경망은 딥 신경망(DNN)이라고 한다. MLP를 훈련시키는 것은 오랫동안 어려운 문제였으나, 1986년 David Rumelhart, Geoffrey Hinton, Ronald Williams가 개발한 역전파(Backpropagation) 훈련 알고리즘이 등장하면서 해결되었다. 역전파 알고리즘은 그래디언트를 자동으로 계산하는 효율적인 기법을 사용하는 경사 하강법의 일종이다. 역전파의 단계는 아래와 같다.
- 미니 배치 단위로 처리하며 전체 훈련 세트를 여러 번 통과한다.(이를 epoch이라 한다.)
- 각 미니 배치는 네트워크의 입력 레이어에 전달되고, 첫 번째 은닉 레이어까지의 모든 뉴런의 출력이 계산된다. 이것이 순방향 전파(forward pass)이며, 예측과 정확한 예측을 위해 중간 결과가 보존된다.
- 알고리즘은 네트워크의 출력 오차를 측정한다.(손실 함수(loss function) 사용)
- 그런 다음 각 출력 연결이 오차에 기여 정도를 계산한다. 이는 이 단계를 빠르고 정확하게 만드는 체인 룰(chain rule)을 적용하여 분석적으로 수행된다.
- 알고리즘은 그런 다음 이 오차 기여의 양이 각 연결에서 나온 것 중 얼마나인지 측정하고, 체인 룰을 다시 사용하여 입력 레이어에 도달할 때까지 이 과정을 반복한다. 이 역방향 전파는 오차 그래디언트를 효율적으로 계산하여 네트워크의 모든 연결 가중치에 걸쳐 오차 그래디언트를 전파시키기 때문에 역전파 알고리즘이라 부른다.
- 마지막으로 알고리즘은 그래디언트 디센트(Gradient Descent) 단계를 수행하여 계산된 오차 그래디언트를 사용하여 네트워크의 모든 연결 가중치를 조정한다.
이 알고리즘이 제대로 작동하려면 우선 모든 은닉 레이어의 연결 가중치를 무작위로 초기화해야 한다. 가중치와 편향을 모두 0으로 초기화하면 해당 레이어의 모든 뉴런이 동일하게 행동하게 되어 역전파가 동일하게 작용하므로 모델이 별로 똑똑하지 않게 된다. 가중치를 무작위로 초기화하면 대칭성을 깨고 역전파가 다양한 뉴런을 훈련시킬 수 있다.
MLP 알고리즘이 제대로 작동하려면 해당 알고리즘의 저자들이 MLP의 구조를 핵심적으로 변경했다. 초기에 사용되던 계단 함수(step function)를 시그모이드(로지스틱) 함수로 교체했다. 시그모이드 함수는 sigma(z) = 1/(1 + exp(-z))로 정의되며, 이 변경은 중요했다. 계단 함수는 완만한 세그먼트만 포함하기 때문에 경사가 없어(경사 하강법이 평평한 표면에서 움직일 수 없음) 문제가 있었는데, 시그모이드 함수는 모든 지점에서 정의된 미분 가능한 도함수를 가지고 있어 경사 하강법이 모든 단계에서 일정한 진전을 만들 수 있게 했다. 사실, 역전파 알고리즘은 로지스틱 함수뿐만 아니라 여러 다른 활성화 함수와도 잘 작동한다. 다른 두 가지 인기 있는 선택지가 있다.
1. 하이퍼볼릭 탄젠트 함수 (tanh): tanh(z) = 2 * sigma(2z) - 1
2. 렐루 함수 (ReLU): ReLU(z) = max(0, z)

역전파 알고리즘은 시그모이드(로지스틱) 함수로 단계를 진행한다. 시그모이드 함수는 모든 지점에서 정의된 미분 가능한 도함수를 가지고 있어 경사 하강법이 평편한 표면에서 움직일 수 있다. 뿐만 아니라 다른 활성화 함수인 하이퍼볼릭 탄젠트 함수와 ReLU 함수도 많이 사용된다. 여러 선형 변환을 연결하면 결국 선형 변환이 되기 때문에 각 레이어 사이에 일정한 비선형성이 필요하다. 활성화 함수 없이는 깊은 신경망이 단일 레이어와 동일하게 작동하게 되어 매우 복잡한 문제를 해결할 수 없다.
Regression MLPs
회귀 작업을 위한 다층 퍼셉트론(MLP)은 예측 모델을 구축하는 데 사용되는데, 여기서 예측은 하나 이상의 출력 값을 갖는 경우를 다룬다. 예를 들어, 집의 여러 특징을 기반으로 주택 가격을 예측하려면 하나의 출력 뉴런을 사용하여 해당 뉴런의 출력이 예측값이 된다. 다변량 회귀의 경우, 각 출력 차원마다 하나의 출력 뉴런이 필요하다. MLP에서 회귀 모델을 구축할 때는 출력 뉴런에 어떤 활성화 함수도 사용하지 않아야 한다. 이는 출력값이 어떤 범위의 값이든 나올 수 있도록 하기 위함이다.
예측값이 항상 양수가 되어야 하는 경우, 출력 레이어에 ReLU 활성화 함수를 사용할 수 있다. 또 다른 옵션으로는 ReLU의 부드러운 변형인 softplus 함수를 사용할 수 있다. 출력값이 특정 범위 내에 있도록 보장하려면 로지스틱 함수나 하이퍼볼릭 탄젠트를 사용하고, 그런 다음 레이블을 해당 범위에 맞게 스케일링하면 된다. 예를 들어, 로지스틱 함수는 0에서 1까지의 범위를 생성하며, 하이퍼볼릭 탄젠트는 -1에서 1까지의 범위를 생성한다. 훈련 중에 사용하는 손실 함수는 주로 평균 제곱 오차(MSE)이지만, 훈련 세트에 이상치가 많은 경우 평균 절대 오차(MAE)를 사용하는 것이 바람직하다. 또는 둘을 조합한 후버 손실(Huber loss)을 사용할 수도 있다. 이러한 손실 함수들은 모델의 예측값과 실제 레이블 간의 차이를 측정하여 모델을 훈련시키는 데 사용된다.
softplus(z) = log(1 + exp(z)).
| 하이퍼파라미터 | 값 |
| # input neurons | 입력 기능(feature) 당 하나(e.g. MNIST의 경우 28 * 28 = 784) |
| # hidden layers | 문제에 따라 다르지만 일반적으로 1 ~ 5 |
| # neurons per hidden layer | 문제에 따라 다르지만 일반적으로 10 ~ 100 |
| # output neurons | 예측 출력(demension) 당 1개 |
| Hidden activation | ReLU(or SELU) |
| Output activation | 없음, 혹은 ReLU/softplus(양수 출력인 경우) 혹은 logistic/tanh(제한된 출력인 경우) |
| Loss function | MSE 혹은 MAE/Huber(이상값인 경우) |
Classification MLPs

이진 분류 문제의 경우 로지스틱 활성화 함수를 사용한 단일 출력 뉴런만으로 충분하다. 이 출력은 0에서 1 사이의 값으로, 이를 긍정 클래스의 추정 확률로 해석할 수 있습니다. 부정 클래스의 추정 확률은 이 값에서 1을 빼면 된다.
다중 레이블 이진 분류 작업 또한 MLP가 쉽게 처리할 수 있다. 예를 들어, 이메일 분류 시스템에서 각 수신 이메일이 스팸인지 여부와 동시에 긴급 또는 긴급하지 않은 이메일인지 예측하는 경우, 로지스틱 활성화 함수를 사용한 출력 뉴런 두 개가 필요합니다. 첫 번째는 이메일이 스팸일 확률을 출력하고, 두 번째는 긴급 여부의 확률을 출력한다. 이 경우 출력 확률이 반드시 1이 되지 않으며, 스팸 또는 긴급하지 않은 스팸 등의 경우가 가능하다.
세 개 이상의 클래스 중 하나에만 속할 수 있는 경우(예: 0부터 9까지의 클래스로 이미지를 분류하는 경우) 클래스당 하나의 출력 뉴런이 필요하며 전체 출력 레이어에는 소프트맥스 활성화 함수를 사용해야 하다. 소프트맥스 함수는 모든 예측 확률이 0에서 1 사이에 있고 합이 1이 되도록 보장하여 클래스가 배타적인 경우에 사용된다. 이를 다중 클래스 분류라고 한다.
손실 함수로는 확률 분포를 예측하므로 교차 엔트로피 손실이 일반적으로 좋은 선택이다.
| 하이퍼파라미터 | 이진 분류 | 다중 레이블 이진 분류 | 다중 클래스 분류 |
| Input and hidden layers | Regression과 같다. | Regression과 같다. | Regression과 같다. |
| # output neurons | 1 | 1 per label | 1 per class |
| Output layer activation | Logistic | Logistic | Softmax |
| Loss function | Cross entropy | Cross entropy | Cross entropy |
Keras로 MLP 구현(Implementing MLPs with Keras)
Sequential API를 사용하여 이미지 분류기 구축

Fashion MNIST는 MNIST와 동일한 형식을 가지고 있으나, 손으로 쓴 숫자 대신 의류 아이템을 나타내는 28x28 픽셀의 70,000개 회색조 이미지이며, 각 클래스는 더 다양하여 더 어려운 문제이다.
fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()
X_train_full.shape # (60000, 28, 28)
X_train_full.dtype # dtype('uint8')
X_valid, X_train = X_train_full[:5000] / 255.0, X_train_full[5000:] / 255.0
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255.0
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat", "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"] Keras를 이용해 데이터셋을 로드하고 검증 세트를 생성하며 입력 특성을 [0, 1]로 스케일링한다.
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape = [28, 28]))
model.add(keras.layers.Dense(300, activation = "relu"))
model.add(keras.layers.Dense(100, activation = "relu"))
model.add(keras.layers.Dense(10, activation = "softmax"))model = keras.models.Sequential([ # 위 예시와 같은 코드
keras.layers.Flatten(input_shape = [28, 28]),
keras.layers.Dense(300, activation = "relu"),
keras.layers.Dense(100, activation = "relu"),
keras.layers.Dense(10, activation = "softmax")
]) 두 개의 은닉층을 가진 분류 MLP를 Sequential API을 사용하여 모델 생성하였다. 첫 번째 줄은 Sequential 모델을 생성한다. 다음으로 첫 번째 층을 빌드하고 모델에 추가한다. 이는 각 입력 이미지를 1D 배열로 변환하는 Flatten 층이다. 그 다음으로는 ReLU 활성화 함수를 사용하는 300과 100 뉴런을 갖는 두 개의 Dense 은닉층을 추가한다. 마지막으로 클래스당 하나의 뉴런을 갖는 10개의 뉴런을 사용하는 Dense 출력 층을 추가하며, 활성화 함수로는 softmax를 사용한다.(클래스가 배타적인 경우)
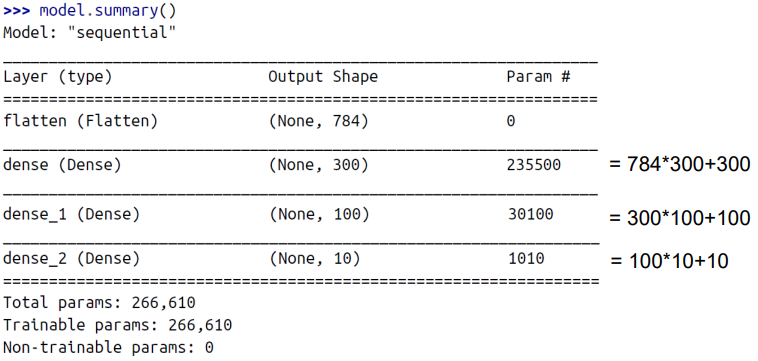
모델의 summary() 메서드는 모델의 모든 층을 표시하며, 각 층의 이름(자동 생성되거나 층을 만들 때 설정한 것), 출력 모양(None은 배치 크기가 어떤 값이든 될 수 있음), 매개변수 수를 표시한다.
입력값이 28 * 28이기에 784, 1번 은닉층은 입력값 784와 300의 출력을 갖고 전부 연결(Dense) 되었기에 784 * 300이다. 여기에 300개의 뉴런은 모두 bias를 가졌기에 300을 더한다. 아래도 같은 과정이다.
hidden1 = model.layers[1]
weights, biases = hidden1.get_weights()
weights #([[0.02448617, -0.00877795, -0.02189048, ..., -0.02766046, 0.03859074, -0.06889391], ..., [-0.06022581, 0.01577859, -0.02585464, ..., -0.00527829, 0.00272203, -0.06793761]],dtype=float32)
weights.shape # (784, 300)
biases # array([0., 0., 0., ..., 0., 0.,0.], dtype=float32)
biases.shape # (300,)Dense 층은 연결 가중치를 무작위로 초기화하고 편향은 0으로 초기화한다.
model.compile(loss = "sparese_categorical_crossentropy", optimizer = "sgd", metrics = ["accuracy"])모델이 생성되면 compile() 메서드를 호출하여 사용할 손실 함수 및 옵티마이저를 지정해야 한다. 추가로 훈련 및 평가 중에 계산할 추가 메트릭 목록을 지정할 수도 있다. sparse_categorical_crossentropy은 희소 레이블이 있으며(즉, 각 인스턴스에 대해 0에서 9까지의 대상 클래스 인덱스만 있음) 클래스가 배타적입이다.

history = model.fit(X_train, y_trian, epochs = 30, validation_data=(X_valid, y_valid))모델을 훈련 및 평가를 할 차례이다. 모델의 성능에 만족하지 않으면 하이퍼파라미터를 조정해야 한다. 학습률 조정, 다른 최적화 시도, 레이어 수, 각 레이어의 뉴런 수, 각 은닉 레이어에 사용할 활성화 함수 등 모델 하이퍼파라미터 조정을 시도할 수 있다.
model.evaluate(X_test, y_test)
검증 정확도에 만족하면 제네럴라이제이션 에러를 추정하기 위해 테스트 세트에서 모델을 평가해야 한다.
X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)
# array([[0., 0., 0., 0., 0., 0., 0.03, 0., 0.01, 0., 0.96],
# [0., 0., 0.98, 0., 0.02, 0., 0., 0., 0., 0., 0.],
# [0., 1, 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
# dtype=float32)
y_pred = model.predict_classes(X_new)
y_pred # array([9, 2, 1])
np.array(class_names)[y_pred] # array([])
y_new = y_test[:3]
y_new # array([9, 2, 1])
모델을 사용하여 예측하기 위해 predict() 메서드를 사용하여 새 인스턴스에 대한 예측을 생성할 수 있다.
Sequential API를 사용하여 Regression MLP 구축
from sklearn.datasets import fetch_california_housingCalifornia 주택 문제를 이용할 것이다. Scikit-Learn의 fetch_california_housing() 함수를 사용하여 데이터를로드한다. numerical feature만 포함하고 ocean_proximity 특성이 없으며 누락된 값이 없다.
model = keras.models.Sequential([])분류와 유사하게 모델을 구축, 훈련, 평가 및 예측에 사용한다. 주요 차이점은 출력 레이어가 단일 뉴런(단일 값 예측)이고 활성화 함수가 없으며 손실 함수가 평균 제곱 오차인 것이다. 데이터셋이 매우 노이지하므로 과적합을 피하기 위해 이전보다 적은 뉴런을 갖는 단일 은닉층만 사용한다.
Functional API를 사용하여 복잡한 모델 구축
input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation="relu")(input_)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.Concatenate(1)([input_, hidden2])
output = keras.layers.Dense(1)(concat)
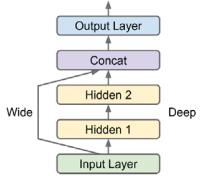
model = keras.Model(inputs=[input_], outputs=[output])비순차 신경망의 한 가지 예는 Wide & Deep 신경망이다. 입력의 전부 또는 일부를 출력 레이어에 직접 연결한다. 위 예시의 아키텍처를 통해 신경망은 딥 패턴(딥 경로 사용)과 간단한 규칙(짧은 경로 사용)을 모두 학습할 수 있다. Keras 모델을 구축하고 나면 모든 것이 이전과 똑같으므로 여기서 반복할 필요가 없다. 그렇기에 모델을 컴파일하고, 훈련하고, 평가하고, 예측에 사용해야 한다.
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.Concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="output")(concat)
model = keras.Model(inputs=[input_A, input_B], output=[output])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:]
X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:]
X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:]
X_new_A, X_new_B = X_test_A[:3], X_test_B[:3]
history = model.fit((X_train_A, X_train_B), y_train, epochs=20, validation_data=((X_valid_A, X_valid_B), y_valid))
mse_test = model.evalute((X_test_A, X_test_B), y_test)
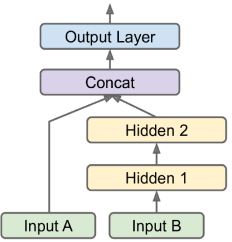
y_pred = model.predict((X_new_A, X_new_B)) 레이어에 연결하여 이 아키텍처를 통해 신경망이 깊은 패턴(깊은 경로 사용)과 간단한 규칙(짧은 경로 사용)을 모두 학습할 수 있다.

output = keras.layers.Dense(1, name="main_output")(concat)
aux_output = keras.layers.Dense(1, name="aux_output")(hidden2)
model = keras.Model(inputs=[input_A, input_B], output=[output, aux_output])
model.compile(loss=["mse","mse"], loss_weights=[0.9, 0.1], optimizer="sgd")
history = model.fit([X_train_A, X_train_B], [y_train, y_train], epochs=20, validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))
total_loss, main_loss, aux_loss = model.evaluate([X_test_A, X_test_B], [y_test, y_test])
y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])여러 가지를 원하는 다중 출력 신경망 사용 사례가 많이 있다. 예를 들어, 작업이 필요할 수 있다. 예를 들어, 사진에서 주요 개체를 찾아 분류하고 싶을 수 있다. 이는 회귀 작업(객체의 중심 좌표와 너비 및 높이 찾기)이자 분류 작업이다. 동일한 데이터를 기반으로 여러 개의 독립적인 작업을 수행할 수 있다. 또 다른 사용 사례는 정규화 기술이다.(즉, 과적합을 줄여 모델의 일반화 능력을 향상시키는 것이 목표인 훈련 제약) 또 다른 예를 들어, 신경망 아키텍처에 일부 보조 출력을 추가하여 네트워크의 기본 부분이 나머지 네트워크에 의존하지 않고 자체적으로 유용한 것을 학습하도록 할 수 있다.
서브클래싱 API(Subclassing API)를 사용하여 동적 모델(Dynamic Models) 구축
Sequential API와 Functional API는 둘 다 선언하여 사용한다. 원하는 레이어와 그들이 어떻게 연결되어야 하는지를 선언한 후에야 모델에 데이터를 제공하여 훈련이나 추론을 시작할 수 있다. 이런 선언적 특징을 가진 API의 장점은 아래와 같다.
- 모델을 쉽게 저장, 복제 및 공유할 수 있다.
- 모델의 구조를 표시하고 분석할 수 있다.
- 프레임워크는 형태를 추론하고 유형을 확인할 수 있어 오류를 빨리 잡을 수 있다.
- 전체 모델이 레이어의 정적 그래프이므로 디버깅이 상대적으로 쉽다.
이런 선언적 특징을 가진 API의 단점으로는 아래와 같다.
- 정적이다.
- 몇몇 모델은 루프, 다양한 형태, 조건 분기 등 동적인 행동이 필요하다.
- 이러한 경우나 더 명령적인 프로그래밍 스타일을 선호하는 경우에는 Subclassing API가 적합하다.
Subclassing API를 사용하려면 Model 클래스를 서브클래싱하고, 필요한 레이어를 생성한 후에 call() 메서드에서 원하는 계산을 수행하면 된다.
# 위와 같은 코드를 클래스화 한 것이다.
class WideAndDeepModel(keras.Moidel):
def __init__(self, units=30, activation="relu", **kwarge):
super().__init__(**kwarge) # 표준 인수 처리
self.hidden1 = keras.layers.Dense(units, activation = activation)
self.hidden2 = keras.layers.Dense(units, activation = activation)
self.main_output = keras.layers.Dense(1)
self.aux_output = keras.layers.Dense(1)
def call(self, inputs):
input_A, input_B = inputs
hidden1 = self.hidden1(input_B)
hidden2 = self.hidden2(input_B)
concat = keras.layers.concatenate([input_A, hidden2])
main_output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return main_output, aux_output
model = WideAndDeepModel()
# 학습된 Keras 모델을 저장
model = keras.models.Sequential([...]) # or keras.Model([...])
model.compile([...])
model.fit([...])
model.save("my_keras_model.h5")
# 모델 불러오기
model = keras.models.load_model("my_keras_model.h5")위 방식을 사용할 때의 장점으로는 call() 메서드 내에서 거의 모든 것을 수행할 수 있다. 반복문, 조건문, TensorFlow의 저수준 연산 등이 가능하다. 반면 모델의 아키텍처가 call() 메서드 내부에 숨겨져 있어 Keras가 쉽게 검사할 수 없으며 저장이나 복제가 어렵고, summary() 메서드를 호출하면 각 레이어의 연결 정보를 얻을 수 없다. 또한 Keras는 미리 유형 및 형태를 확인할 수 없으며, 실수하기가 더 쉽다.
모델 저장 및 복원
H5 파일은 계층적 데이터 형식(Hierarchical Data Format, HDF)으로 저장된 파일의 확장자이다. 이 파일 형식은 대량의 데이터를 저장하고 관리하는 데 사용되며, 주로 과학 및 공학 분야에서 데이터를 저장하고 교환하는 데 널리 사용된다. H5 파일은 다양한 유형의 데이터를 저장할 수 있으며, 대규모의 복잡한 데이터 구조도 지원한다. 이를 사용하는 이유로는 계층 구조 저장하기 위해, 다양한 데이터 형식을 지원되고, 대용량 데이터 처리에 유용하며, 이식성, 압추그 청크가 뛰어나고 메타 데이터 관리에 유용하다. 따라서 H5 파일은 다양한 종류의 데이터를 효율적으로 저장하고 관리하기 위한 강력한 도구로 사용된다.
- 계층 구조 저장: H5 파일은 데이터를 계층 구조로 저장할 수 있다. 이는 데이터를 효과적으로 구조화하고 정리할 수 있게 해주며, 다양한 유형의 데이터를 계층적으로 저장할 수 있다.
- 다양한 데이터 형식 지원: H5 파일은 숫자, 텍스트, 이미지, 테이블 등과 같은 다양한 데이터 형식을 지원한다. 따라서 다양한 유형의 데이터를 하나의 파일에 저장할 수 있다.
- 대용량 데이터 처리: H5 파일은 대용량의 데이터를 효과적으로 저장할 수 있는 구조를 가지고 있다. 이는 과학적 실험 결과, 시뮬레이션 결과 등과 같이 대량의 데이터를 다루는 데 유용하다.
- 포터블한 형식: H5 파일은 이식성이 뛰어나며, 여러 플랫폼 및 프로그래밍 언어에서 읽고 쓸 수 있다. 이는 데이터를 쉽게 교환하고 공유할 수 있게 해준다.
- 압축 및 청크 처리: H5 파일은 데이터를 압축하고 청크 단위로 처리할 수 있다. 이는 디스크 공간을 절약하고 데이터 읽기/쓰기 속도를 향상시킬 수 있다.
- 메타데이터 관리: H5 파일에는 메타데이터를 추가하여 데이터에 대한 설명이나 주석을 포함할 수 있다. 이는 데이터를 이해하고 관리하는 데 도움이 된다.
콜백(Callbacks) 사용
[...] # 모델 빌드와 컴파일
checkpoint_cb = keras.callback.ModelCheckint("my_keras_model.h5")
history = model.fit(X_train, y_train, epochs = 10, callbacks=[checkpoint_cb])
checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5", save_best_only=Ture)
history = model.fix(X_train, y_train, epochs = 10, validation_data = (X_valid, y_valid), callbacks=[checkpoint_cb])
model = keras.models.load_model("my_keras_model.h5") # best 모델로 롤백`fit()` 메서드는 훈련 시작 및 종료, 각 에포크의 시작 및 종료, 심지어 각 배치 처리 전후에 Keras가 호출할 수 있는 객체 목록을 지정할 수 있는 `callbacks` 인자를 허용한다. 예를 들어, ModelCheckpoint 콜백을 사용하면 기본적으로 각 에포크의 끝에서 모델의 체크포인트를 정기적으로 저장할 수 있다. 또한 훈련 중에 검증 세트를 사용하는 경우, ModelCheckpoint를 생성할 때 save_best_only=True를 설정하여 검증 세트에서의 성능이 지금까지 가장 우수할 때만 모델을 저장할 수 있다. 조기 종료를 구현하는 또 다른 방법은 EarlyStopping 콜백을 사용하는 것이다. 이 콜백은 검증 세트에서 일정 에포크 동안 진전이 없을 경우 (patience 인자로 정의됨) 훈련을 중단하고 선택적으로 최적의 모델로 롤백한다.
class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print("\nval/train: {:.2f}".format(logs["val_loss"] / logs["loss"]))사용자 지정 콜백을 쉽게 작성할 수 있습니다. 아래의 예시는 훈련 중에 검증 손실과 훈련 손실 간의 비율을 표시하는 사용자 지정 콜백이다. 이외에도 콜백은 평가 및 예측 중에도 활용될 수 있다.
사용자 지정 콜백은 `on_train_begin()`, `on_train_end()`, `on_epoch_begin()`, `on_epoch_end()`, `on_batch_begin()`, `on_batch_end()`를 구현할 수 있다.
평가를 위해 `on_test_begin()`, `on_test_end()`, `on_test_batch_begin()`, `on_test_batch_end()` (evaluate()에 의해 호출)를 구현할 수 있다.
예측을 위해 `on_predict_begin()`, `on_predict_end()`, `on_predict_batch_begin()`, `on_predict_batch_end()` (predict()에 의해 호출)를 구현할 수 있다.
시각화(Visualization)를 위해 텐서보드(TensorBoard) 사용
TensorBoard는 학습 중인 학습 곡선을 확인하고 여러 실행 간의 학습 곡선을 비교하며 계산 그래프를 시각화하며 훈련 통계를 분석하고 모델이 생성한 이미지를 확인하며 복잡한 다차원 데이터를 3D로 투영하고 클러스터링하는 등 다양한 기능을 제공하는 대화형 시각화 도구이다.
프로그램을 수정하여 특별한 이진 로그 파일인 이벤트 파일에 시각화하려는 데이터를 출력해야 한다. 각 이진 데이터 레코드는 summary라고 불린다. TensorBoard 서버는 로그 디렉토리를 모니터링하고 변경 사항을 자동으로 감지하고 시각화를 업데이트합니다. 이를 통해 실시간 데이터를 시각화할 수 있다.
import os
root_logdir = os.path.join(os.curdir, "my_logs")
def get_run_logdir():
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir()
[...] # 모델 빌드와 컴파일 과정
tensorboard_cb = keras.callback.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs = 30, validation_data = (X_valid, y_valid), callbacks=[tensorboard_cb])먼저 TensorBoard 로그에 사용할 루트 로그 디렉토리를 정의하고 현재 날짜와 시간을 기반으로 서브디렉토리 경로를 생성하는 작은 함수를 정의한다. Keras는 TensorBoard 콜백을 지원한다. 이 코드를 실행하면 TensorBoard 콜백이 로그 디렉토리를 생성하고(필요한 경우 상위 디렉토리와 함께) 훈련 중에 이벤트 파일을 생성하고 이에 요약을 기록하였다.
# 터미널에서 실행해야한다.
tensorboard --logdir=./my_logs --port=6006다음으로 TensorBoard 서버를 시작해야 한다. 이를 위해 터미널에서 명령을 실행해야 한다. TensorFlow를 가상환경에서 설치한 경우 활성화해야 한다. 그런 다음 프로젝트의 루트에서 다음 명령을 실행한다(또는 다른 곳에서 실행하되 적절한 로그 디렉토리를 가리켜야 한다).
load_ext tensorboard
tensorboard --logdir=./my_logs - port=6006서버가 실행되면 웹 브라우저를 열고 http://localhost:6006로 이동할 수 있다. 또는 Jupyter 내에서 직접 TensorBoard를 사용하려면 위와 같은 명령을 실행한다.
뉴런 네트워크 하이퍼파라미터 미세 조정
신경망의 유연성은 그들의 주요 단점 중 하나이기도 하다. 왜냐하면 조절해야 할 하이퍼파라미터가 너무 많기 때문이다. 층의 수, 각 층당 뉴런의 수, 각 층에서 사용할 활성화 함수의 종류, 가중치 초기화 로직 등이 있다. 하이퍼파라미터을 탐색하는 단순한 방법 중 하나는 하이퍼파라미터 조합을 시도하고 검증 세트에서 최상의 성능을 내는 것이다. 또는 K-fold 교차 검증을 사용할 수도 있다. Scikit-Learn의 GridSearchCV 또는 RandomizedSearchCV를 사용하여 하이퍼파라미터 공간을 탐색하려면 Keras 모델을 일반적인 Scikit-Learn 회귀기와 유사한 객체로 래핑해야 한다.
def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
model = kears.models.Sequential()
model.add(keras.layers.InputLayer(input_shape = input_shape))
for layer in range(n_hidden):
model.add(keras.layers.Dense(n_nerons, activation="relu"))
model.add(keras.layers.Dense(1))
optimizer = keras.optimizers.SGD(lr=learning_rate)
model.compile(loss="mse", optimizer = optimizer)
return model
keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model)
keras_reg.fit(X_train, y_train, epochs=100, validation_data=(X_valid, y_valid), callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)먼저, 주어진 하이퍼파라미터 세트에 기반하여 Keras 모델을 생성하고 컴파일하는 함수를 만들어야 한다. 다음으로, 이 `build_model()` 함수를 기반으로 한 KerasRegressor를 생성합니다. 이렇게 생성된 이 객체를 일반적인 Scikit-Learn 회귀기처럼 사용할 수 있습니다. `fit()` 메서드를 사용하여 훈련하고, `score()` 메서드를 사용하여 평가하며, `predict()` 메서드를 사용하여 예측할 수 있다.
from scipy.stats import reciprocal
from sklearn.model_selection import RandomizeSearchCV
param_distribs = {
"n_hidden": [0, 1, 2, 3],
"n_neurons": np.arange(1, 100),
"learning_rate": reciprocal(3e-4, 3e-2),
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3)
rnd_search_cv.fit(X_train, y_train, epochs=100, validation_data=(X_valid, y_valid), callbacks=[keras.callbacks.EarlyStopping(patiense=10)])
rnd_search_cv.best_params_
# {'learning_rate': 0.003362541252688094, 'n_hidden': 2, 'n_neurons': 42}
rnd_search_cv.best_score_
# -0.3189529188278931
model = rnd_search_cv.best_estimator_.model 위 코드를 살펴보면 은닉층 수, 각 층의 뉴런 수 및 학습률을 탐색해 볼 수 있다.. 탐색이 완료되면 다음과 같이 찾은 최적의 매개변수, 최고 점수 및 훈련된 Keras 모델에 액세스할 수 있다.
무작위보다 효율적으로 검색 공간을 탐색하는 다양한 기술이 있다. Hyperopt, Hyperas, kopt, Talos, Kears Tuner, Scikit-optimize, Spearmint, Hyperband, Sklearn-Deap 등의 파이썬 라이브러리가 있다. 하이퍼파라미터 조정은 여전히 활발한 연구 분야이며, evolutionary 알고리즘도 부활하고 있다. DeepMind은 2017년에 모델과 하이퍼파라미터 모두를 공동으로 최적화하는 방식으로 evolutionary 알고리즘을 적용했으며, Google은 AutoML이라는 진화적 접근법을 사용하여 하이퍼파라미터뿐만 아니라 문제에 대한 최상의 신경망 아키텍처를 찾기도 했다.
Number of Hidden Layers
은닉층의 수에 대한 결정은 특정 문제와 데이터에 따라 다르지만, 일반적으로 하나 또는 두 개의 은닉층으로 충분할 수 있다. MNIST와 같은 간단한 작업에서는 적은 수의 뉴런을 가진 은닉층으로도 높은 정확도를 달성할 수 있다. 그러나 더 복잡한 작업이나 대규모 데이터셋의 경우 수십 개의 층이 필요할 수 있다.
은닉층의 크기는 일반적으로 처음 은닉층에서는 더 많은 뉴런을 사용하는 피라미드 모양(뉴런의 수가 점점 줄어들도록 설정)으로 설정되었으나, 이러한 방식은 현재는 덜 선호되고 있다. 대부분의 경우 모든 은닉층에 동일한 수의 뉴런을 사용하는 것이 성능 면에서 비슷하거나 더 나은 결과를 낼 수 있다. 첫 번째 은닉층을 다른 층보다 크게 만들어 사용하는 경우도 있다.
또한 네트워크의 깊이와 너비를 튜닝하기 위해 하이퍼파라미터 탐색이 필요한데, 이를 위해 GridSearchCV 또는 RandomizedSearchCV와 같은 도구를 사용할 수 있다. 하이퍼파라미터 튜닝은 여전히 연구 중이며, 다양한 라이브러리 및 알고리즘이 제안되고 있다.
Learning Rate, Batch Size, and Other Hyperparameters
학습률(Learning Rate), 옵티마이저(Optimizer), 활성화 함수(Activation Function), 그리고 배치 크기(Batch Size)는 신경망의 성능에 중요한 영향을 미치는 하이퍼파라미터이다.
- 학습률 (Learning Rate): 학습률은 가장 중요한 하이퍼파라미터로 여겨진다. 일반적으로 최적의 학습률은 최대 학습률의 약 절반 정도이다.
- 옵티마이저 (Optimizer): 미니배치 경사 하강법 이상의 향상된 옵티마이저를 선택하고 해당 하이퍼파라미터를 조정하는 것도 중요하다.
- 활성화 함수 (Activation Function): 일반적으로 ReLU 활성화 함수가 숨겨진 레이어에 대한 좋은 기본값이다. 출력 레이어에 대해서는 작업에 따라 다를 수 있다.
- 반복 횟수 (Number of Iterations): 대부분의 경우 반복 횟수를 조정할 필요가 없다. 대신 조기 종료(early stopping)를 사용하면 된다.
- 배치 크기 (Batch Size): 큰 배치 크기의 주요 이점은 GPU와 같은 하드웨어 가속기가 효율적으로 처리할 수 있어 초당 더 많은 인스턴스를 처리할 수 있다는 것이다. 그러나 큰 배치 크기는 특히 훈련 초기에 불안정성을 초래하며 결과 모델이 작은 배치 크기로 훈련된 모델만큼 일반화되지 않을 수 있다. 다양한 논문들이 다른 방향을 제시한다. 일부는 작은 배치 크기를 권장하고, 다른 연구에서는 학습률을 조절하는 등의 기술을 사용하여 매우 큰 배치 크기를 사용할 수 있다고 보고했다. 따라서 큰 배치 크기를 시도하고 훈련이 불안정하거나 최종 성능이 기대에 못 미치는 경우 작은 배치 크기를 대신 시도하는 전략을 취할 수 있다.
참고
모듈 공식 문서 및 치트 시트를 아래 페이지에 정리해놨다.
8.모듈
서론 파이썬에는 기본 탑재된 함수나 다른 사람이 만든 함수나 변수들을 불러 사용할 수 있다. 이런 기능들이 있기에 파이썬이 다재다능해질 수 있는다. 모듈 모듈이란 함수나 변수 등을 모아
jinger.tistory.com
'컴퓨터공학 > AI' 카테고리의 다른 글
| 기계학습 12. Convolutional Neural Networks(CNN) (0) | 2023.12.12 |
|---|---|
| 기계학습 11. Training Deep Neural Networks (1) | 2023.12.01 |
| 기계 학습 9. Unsupervised Learning Techniques (1) | 2023.11.17 |
| 기계 학습 8. 차원 축소(Dimensionality Reduction) (0) | 2023.10.28 |
| 기계 학습 7. Ensemble Learning and Random Forests (1) | 2023.10.20 |




댓글