서론
AI를 배우는 데 많은 수학적 이론을 알아둬야 한다. 그 중 다른 타 수학 이론과 달리 행렬은 대한민국 교육과정에서 빠져 행렬을 정리해보았다.
벡터란?
여태까지 사용한 숫자는 스칼라이다. 스칼라 (scalar)란 차원(dimension)이 없는 숫자를 의미한다. 반면 벡터 (vector)란 개의 숫자 모음 ( 차원 벡터), "크기" 와 "방향" 이 같으면, 같은 벡터를 의미한다. 여기서 나오는 법칙이 바로 벡터의 동등성 원칙이다. 두 벡터가 같다면 벡터의 크기가 같고, 방향이 같음을 의미한다.
벡터가 왜 인공지능에서 중요하냐면 학습하는 데이터 "상대적"인 위치가 크기보다 더 중요하기 때문이다.
벡터 연산
벡터의 연산은 아래와 같이 이루어진다.




벡터 내적
벡터 내적은 두 벡터 간에 대응하는 성분들을 곱한 후 그 결과를 모두 더하여 구한다. 만약에 두 벡터가 a = (a_1, a_2) 와 b = (b_1, b_2) 라고 한다면, 두 벡터의 내적은 다음과 같이 계산됩니다.
a*b = a_1*b_1 + a_2*b_2
내적은 두 벡터가 얼마나 같은 방향을 향하고 있는지, 또는 한 벡터가 다른 벡터의 방향으로 얼마나 빠르게 증가하는지를 나타낸다.

벡터의 크기는 두 점사이의 거리처럼 계산이 이루어진다. 단, 차원의 수만큼 제곱근을 씌워야한다. 특히, 단순히 제곱하는 L norm(크기)을 손실함수로 많이 사용하지만, 0 근처에서 학습이 느리다는 특징이 있다.
벡터 크기




두 점을 지나는 직선을 벡터를 이용하여 표시하는 이유는 데이터를 저장 및 처리하는 과정에서 다차원으로 저장이 되는 데, 벡터가 다차원으로 확장이 용이하기 때문이다.

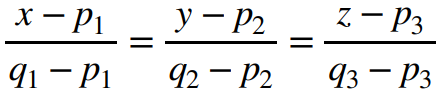
다차원에서 벡터
평면의 방정식에서 법선 벡터(평면에 수직인 벡터, normal vector)를 활용한 평면의 방정식을 아래와 같이 행렬로 해석할 수 있다.

이렇듯 행렬은 벡터를 선형 변환시키는 역할을 수행한다. 즉, 다차원 데이터를 쉽게 다루기 위해 행렬을 사용한다.




아핀변환
아핀 변환이란 두 점을 매핑하는 변환이며, 이때 한 점을 다른 점으로 옮기는데 선형 변환이 사용되고, 이후에 이동 변환을 통해 다른 점으로 이동시킨다. 즉, 아핀 변환은 선형 변환과 이동으로 이루어진 변환이며, 선형 변환은 벡터 공간에서의 선형 관계를 유지시키는 변환을 말한다. 이러한 변환은 벡터의 선형 조합을 통해 이루어진다. 아핀 변환은 이러한 선형 변환에 이동 변환을 추가하여 구성된다.
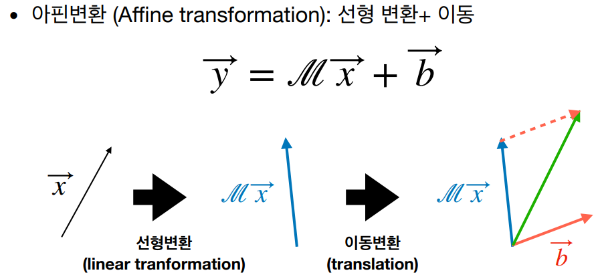
아핀변환의 특성으로 평행한 선분들은 평행한 선분들로 옮길 수 있다.
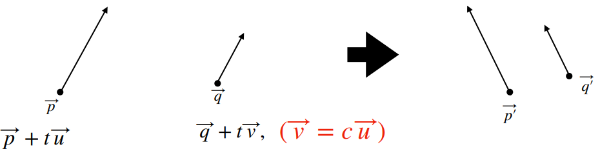
행렬
행렬은 일반적으로 n 차원 벡터를 m 차원 벡터로 변환 시킬 때 사용된다.



전치행렬 (Transpose)
전치 행렬(Transpose Matrix)은 기존 행렬의 행과 열을 대칭하게 바꾼 새로운 행렬을 의미한다. 즉, 주어진 행렬의 행은 열이 되고, 열은 행이 된다. 전치 행렬은 주어진 행렬을 A라고 할 때 A⊤로 표시한다.

대칭 행렬에서 주목해야할 점은 대칭행렬의 고유값이 서로다른 고유벡터들은 서로 직교한다는 점이다.
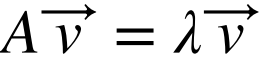
행렬의 일반화: 텐서
행렬은 차원(축, axis) 이 2개 이상인 배열 표현하는 데 특화되어 있다. 특히 행렬은 2차원 행렬을 일반화 시켜, 수들의 배열을 표시한 것이다. 아래 예시처럼 4차원으로 값을 저장할 때 (0-tensor: 스칼라 1-tensor: 벡터 2-tensor: 행렬 3-tensor: 이미지 4-tensor: 영상) 이러한 식으로 저장 및 표현할 수 있다.

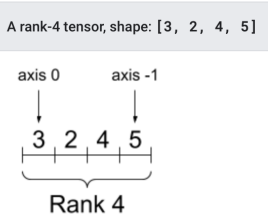
주섬주섬
인공지능에서 사용된 행렬 개념을 쉽게 이해하기 위해 핵심적인 개념만 가져왔다.
'컴퓨터공학 > AI' 카테고리의 다른 글
| 인공지능 2. 기초 최적화 이론 (0) | 2024.04.05 |
|---|---|
| 인공지능 1. 퍼셉트론 (0) | 2024.04.01 |
| 기계학습 12. Convolutional Neural Networks(CNN) (0) | 2023.12.12 |
| 기계학습 11. Training Deep Neural Networks (1) | 2023.12.01 |
| 기계학습 10. Introduction to Artificial Neural Networks(ANN) (0) | 2023.12.01 |




댓글